Basic Information

Authors: Marwa El Halabi, Suraj Srinivas, Simon Lacoste-Julien

Organization: Samsumg, Harvard University

Source: NeurIPS 2022

Source Code: https://github.com/marwash25/subpruning

Cite: El Halabi, Marwa, Suraj Srinivas, and Simon Lacoste-Julien. “Data-efficient structured pruning via submodular optimization.” Advances in Neural Information Processing Systems 35 (2022): 36613-36626.

Content

Motivation

Existing pruning methods fall into two main categories: unstructured pruning methods which prune individual weights leading to irregular sparsity patterns, and structured pruning methods which prune regular regions of weights, such as neurons, channels, or attention heads. Structured pruning methods are generally preferable as the resulting pruned models can work with off-the-shelf hardware or kernels, as opposed to models pruned with unstructured pruning which require specialized ones.

The majority of existing structured pruning methods are heuristics that do not offer any theoretical guarantees. Moreover, most pruning methods are inapplicable in the limited-data regime, as they rely on fine-tuning with large training data for at least a few epochs to recover some of the accuracy lost with pruning. [1] proposed a “reweighting” procedure applicable to any pruning method, which optimize the remaining weights of the next layer to minimize the change in the input to the next layer. Their empirical results on pruning single linear layers suggest that reweighting can provide a similar boost to performance as fine-tuning, without the need for data labels.

The optimization with respect to the weights, for a fixed selection of neurons, is the same one used for reweighting in [1]. The resulting subset selection problem is intractable, but we show that it can be formulated as a weakly submodular maximization problem (see Definition 2.1).

We can thus use the standard greedy algorithm to obtain an approximation to the optimal solution, where is non-zero if we use sufficient training data. We further adapt our method to prune any regular regions of weights; we focus in particular on pruning channels in convolution layers. To prune multiple layers in the network, we apply our method to each layer independently or sequentially.

Evaluation

Baselines:

1. LayerGreedyFS: for each layer, first removes all neurons/channels in that layer, then gradually adds back the neuron/channel that yields the largest decrease of the loss, evaluated on one batch of training data. Layers are pruned sequentially from the input to the output layer.
2. LayerSampling: samples neurons/channels, in each layer, with probabilities proportional to sensitivities based on (activations $\times$ weights), and prunes the rest.
3. ActGrad: prunes neurons/channels with the lowest (activations $\times$ gradients), averaged over the training data, with layerwise $l_2$-normalization.
4. LayerActGrad: prunes neurons/channels with the lowest (activations $\times$ gradients), averaged over the training data, in each layer. This is the layerwise variant of ACTGRAD.
5. LayerWeightNorm: prunes neurons/channels with the lowest output weights $l_1$-norm, in each layer.
6. Random: prunes randomly selected neurons/channels globally across layers in the network.
7. LayerRandom: prunes randomly selected neurons/channels in each layer.

Metric: top-1 accuracy, compression ratio

Datasets

LetNet on MNIST, ResNet56 on CIFAR-10, VGG11 on CIFAR10. (Pre-trained)

Result

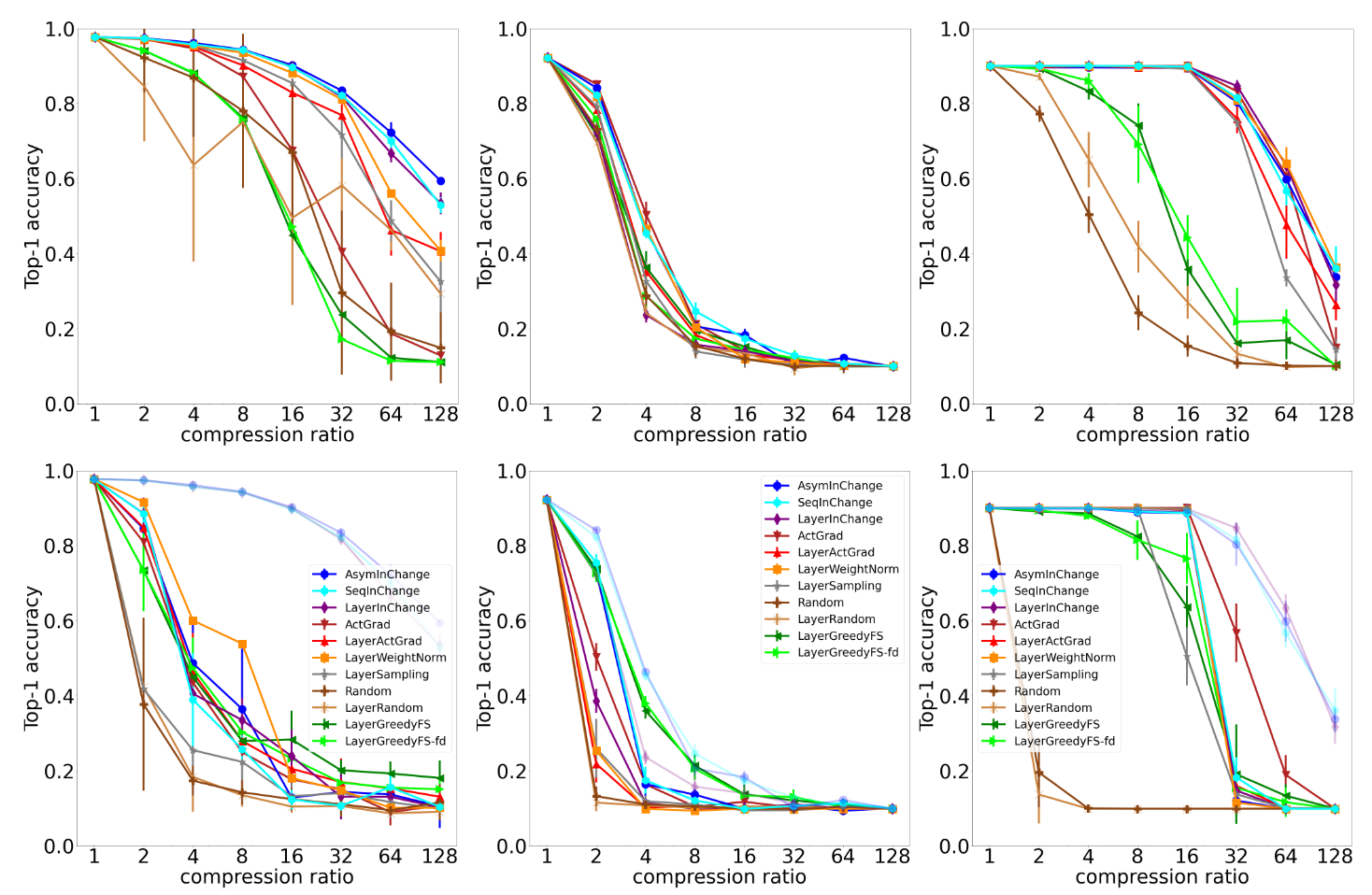
Figure 2. Top-1 Accuracy of different pruning methods applied to LeNet on MNIST (left), ResNet56 on CIFAR10 (middle), and VGG11 on CIFAR10 (right), for several compression ratios (in log-scale), with (top) and without (bottom) reweighting. We include the three reweighted variants of our method in the bottom plots (faded) for reference.

Preliminaries

Notation

Given a ground set $V = \lbrace 1, 2, ··· ,d \rbrace$ and a set function $F:2^V \rightarrow R_+$, we denote the marginal gain of adding a set $I \subseteq V$ to another set $ S \subseteq V$ by $F(I | S) = F(S \cup I) -F(S)$, which quantifies the change in value when adding $I$ to $S$. The cardinality of a set $S$ is written as $|S|$. Given a vector $x \in R^d$, we denote its support set by $supp(x)=\lbrace i \in V | x_i \neq 0 \rbrace$ , and its $l_2$-norm by $||x||_2$. Given a matrix $X \in R^{d’\times d}$, we denote its $i$-th column by $X_i$, and its Frobenius norm by $||X||_F$ . Given a set $ S \subseteq V$ , $X_S$ is the matrix with columns $X_i$ for all $i \in S$, and 0 otherwise, and $\mathbf{1}_S$ is the indicator vector of $S$, with $[\mathbf{1}_S]_i =1$for all $i \in S$, and 0 otherwise.

weakly submodular maximization

A set Function $F$ is submodular if it has diminishing marginal gains: $F(i|S) \ge F(i|T)$ for all $S \subseteq T$, $i \in V \backslash T$. We say that $F$ is normalized if $F(\emptyset)=0$, and non-decreasing if $F(S) \le F(T)$ for all $S \subseteq T$.

Given a non-decreasing submodular function $F$ , selecting a set $S \subseteq V$ with cardinality $\mid S \mid \le k$ that maximize $F(S)$ can be done efficiently using the Greedy algorithm Algorithm 1. The returned solution is guaranteed to satisfy $F(\hat S) \ge (1 - 1/e) \mathrm{max}_{\mid S \mid \le k} F(S)$

In general though maximizing a non-submodular function over a cardinality constraint is NP-Hard. However, Das and Kempe introduced a notion of weak submodularity which is sufficient to obtain a constant factor approximation with the Greedy algorithm.

Given a set function $F:2^V \rightarrow \mathbb{R}$,$U \subseteq V$, $k \in \mathbb{N}+$, we say that $F$ is $\gamma_{U,k}$-weakly submodular, with $\gamma_{U,k} > 0$ if

for every two disjoint sets $L, S \subseteq V$, such that $L \subseteq U$, $\mid S \mid \le k$. The parameter $\gamma_{U,k}$ is called the submodularity ratio of $F$. It characterizes how close a set function is to being submodular. If $F$ is non-decreasing then $\gamma_{U,k} \in [0, 1]$, and $F$ is submodular if and only if $\gamma_{U,k} = 1$ for all $U \subseteq V$, $k \in \mathbb{N}+$. Given a non-decreasing $\gamma_{\hat{S},k}$-weakly submodular function $F$, the Greedy algorithm is guaranteed to return a solution $\hat{S}$ satisfying $F(\hat{S}) \ge (1 - e^{-\gamma_{\hat{S},k}})\mathrm{max}_{\mid S \mid \le k} F(S)$. Hence, the closer $F$ is to being submodular, the better is the approximation guarantee.

Method

Given a large pretrained NN, $n$ training data samples, and a layer $l$ with $n_l$ neurons, our goal is to select a small number $k$ out of the $n_l$ neurons to keep, and prune the rest, in a way that influences the network the least. However, simply throwing away the activations from the dropped neurons is wasteful. Instead, we optimize the weights of the next layer to reconstruct the inputs from the remaining neurons.

Formally, let $A^l \in \mathbb{R}^{n \times n_l}$ be the activation matrix of layer $l$ with columns $a^l_1, \dots, a^l_{n_l}$, where $a_i^l \in \mathbb{R^n}$ is the vector of activations of the $i$th neuron in layer $l$ for each training input, and let $W^{l+1} \in \mathbb{R}^{n_l \times n_{l+1}}$ be the weight matrix of layer $l+1$ with columns $w_1^{l+1}, \dots, w_{n_{l+1}}^{l+1}$, where $w_i^{l+1} \in \mathbb{R}^{n_l}$ is the vector of weights connecting the ith neuron in layer $l+1$ o the neurons in layer $l$. When a neuron is pruned in layer $l$, the corresponding column of weights in $W^l$ and the row in $W^{l+1}$ are removed.

Let $V_l = \lbrace 1, \dots, n_l \rbrace$. Given a set $S \subseteq V_l$, we denote by $A_S^l$ the matrix with columns $a_i^l$ for all $i\in S$, and 0 otherwise. We choose a set of neurons $S \subseteq V_l$ to keep new weights $\tilde W^{l+1} \in \mathbb{R}^{n_l \times n_{l+1}}$ that minimize:

Greedy selection

we show below that it can be formulated as a weakly submodular maximization problem, hence it can be efficiently approximated. Let

The problem is equivalent to $\mathrm{max}_{\mid S \mid \le k} F(S)$

Given $U \subseteq V$, $k \in \mathbb{N}+$, $F$ is a normalized non-decreasing $\gamma_{U,k}$-weakly submodular function, with

We use the GREEDY algorithm to select a set $\hat{S} \subseteq V_l$ of $k$ neurons to keep in layer $l$. the returned solution is guaranteed to satisfy

Comments

Pros

todo

Cons

(need further experiment)

Further work

todo

Comments

(need further experiment)

References

[1] Z. Mariet and S. Sra. Diversity networks: Neural network compression using determinantal point processes. arXiv preprint arXiv:1511.05077, 2015.