Basic Information
Authors: Xuesong Chen, Shaoshuai Shi, Benjin Zhu, Ka Chun, Cheung, Hang Xu, and Hongsheng Li
Organization: MMLab CUHK, MPI-INF, HKBU, Huawei Noah’s Ark Lab
Source: ECCV 2022
Source Code: https://github.com/open-mmlab/OpenPCDet
Cite: Chen, Xuesong, et al. “MPPNet: Multi-Frame Feature Intertwining with Proxy Points for 3D Temporal Object Detection.” Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part VIII. Cham: Springer Nature Switzerland, 2022.
Content
Motivation
LiDAR sensors can only produce point clouds to capture one partial view of the scene at a time. This characteristic leads to incomplete point distributions of objects in driving scenes.
Recently, several approaches [1,2,3] have demonstrated that a simple concatenation of multi-frame point clouds can significantly improve the performance over single-frame detection. However, this strategy is only suitable for handling very short sequences (e.g., 2-4 frames), and its performance might even drop when used to process more frames, as shown in Table 1, since the fused point clouds of long sequences might show “tails” of different visual patterns from different moving objects, posing additional challenges to the detectors.

Table 1. Pilot experiments of CenterPoint on Waymo validation set in terms of mAPH (LEVEL 2) of the vehicle class by taking concatenated point clouds as input.
We propose a novel two-stage 3D detection framework, named MPPNet, to effectively integrate features from Multi-frame point clouds via Proxy Points for achieving more accurate 3D detection results. The first stage adopts existing single-stage 3D detectors to generate 3D proposal trajectories, and we mainly focus on the second stage that takes a 3D proposal trajectory as input to aggregate multi-frame features in an object-centric manner for estimating more accurate 3D bounding boxes. The key idea of our approach is a series of inherently aligned proxy points to encode consistent representations of an object over time and a three-hierarchy paradigm for better fusing long-term feature sequences.
Evaluation
Metric: 3D AP/APH
Baselines: RSN[2], 3D-MAN[4], Centerpoint[3], CT3D-MF[5]
Datasets
Waymo
Result
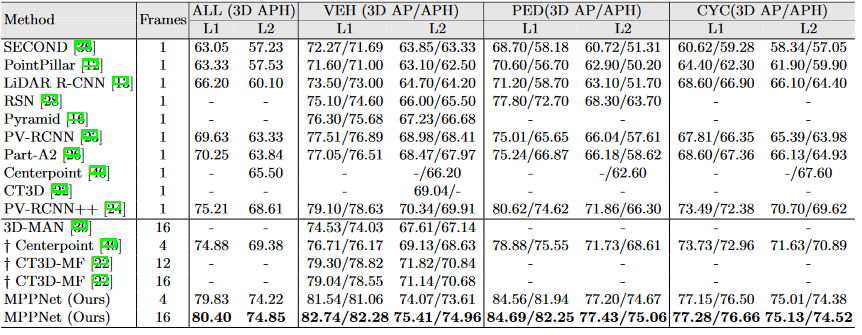
Table 2. Performance comparison on the validation set of Waymo Open Dataset. † indicates the method implemented by us. The Centerpoint with 4-frame input is adopted as MPPNet’s 1st-stage.

Table 3. Performance comparison on the testing set of Waymo Open Dataset.
Method
Most state-of-the-art 3D detection approaches adopt a simple concatenation strategy [3] to take multi-frame point clouds as input for improving 3D temporal detection, which are generally effective at handling short point cloud sequences but fail to deal with long sequences due to the challenge of point-cloud trajectories with different moving patterns. 3D-MAN [4] utilizes the attention networks to aggregate multi-frame features, which, however, may attend to mismatched proposals due to the dense connections among all proposals.
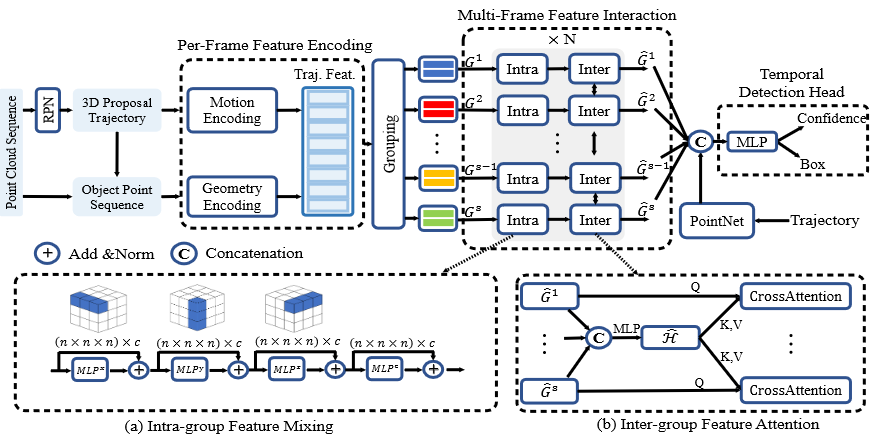
Figure. 1. The overall architecture of our proposed MPPNet. Our approach takes a point cloud sequence as input for temporal 3D object detection, where a three-hierarchy model is proposed for the multi-frame feature encoding and interaction.
We propose MPPNet, a two-stage 3D detection framework, which takes the point cloud sequences as input to greatly improve the detection results. In the first stage, we adopt existing single-stage 3D detectors to generate 3D proposal trajectories. Our main innovation focuses on the second stage that takes a 3D proposal trajectory as input and effectively aggregates the multi-frame object features for predicting more accurate 3D bounding boxes.
Single-frame Proposal Network and 3D Proposal Trajectories
Given a point cloud sequence, we create consecutive 4-frame clips and extend the single-stage 3D detectors [3] as [2] to generate per-frame 3D detection boxes.
To associate the 3D detection boxes as 3D proposal trajectories, we add an extra speed prediction head for estimating the speeds of the detected objects, where the speeds are utilized to associate the 3D proposal boxes with a predefined Intersection-over-Union (IoU) threshold as in [3].
After associating per-frame 3D proposal boxes to create a 3D proposal trajectory, let $\lbrace B^1, \dots, B^T \rbrace$ denote the T -frame 3D proposal trajectory and $K^t = \lbrace l_1^t, \dots, l_m^t \rbrace_{t = 1,\dots, T} $ denote object points region pooled [6] from each frame t. They are input into the second stage of our framework for multi-frame feature encoding and interaction to generate more accurate a 3D bounding box.
Three-Hierarchy Feature Aggregation with Proxy Points
We propose to adopt a set of inherently aligned proxy points at each frame, which not only provide consistent per-frame representations for the object points, but also facilitate multi-frame feature interaction by serving as the courier for cross-time propagation. With the proxy points, we further present a three-hierarchy model to effectively aggregate multi-frame features from the object point sequence for improve the performance of 3D detection, where the first hierarchy encodes the per-frame object geometry and motion features in a decoupled manner, the second hierarchy performs the feature mixing within each short clip (group) and the third hierarchy propagates whole-sequence information among all clips. By alternatively stacking the intragroup and inter-group feature interactions, the multi-frame features can be well summarized to achieve more accurate detection.
Proxy Points.
The proxy points are placed at fixed and consistent relative positions in each 3D proposal box of the proposal trajectory. Specifically, at each time t, $N = n \times n \times n$ proxy points are uniformly sampled within the 3D proposal box and are denoted as $P^t = \lbrace p_1^t, \dots, p_N^t \rbrace$. These proxy points maintain the temporal order as the order of the trajectory boxes. As they are uniformly sampled in the same way across time, they naturally align the same spatial parts of the object proposals over time.
Decoupled per-frame feature encoding.
Our first hierarchy performs perframe feature encoding. The object geometry and motion features are separately encoded based on the proxy points as illustrated in Fig. 2 (b).
For encoding geometry features with proxy points, the relative differences between each object point $l_i^t \in K^t$ and the 8 corner + 1 center points of the proposal box $B^t = \lbrace b_j^t \rbrace_{j=1}^9$ are first calculated as
\[\Delta l_i^t = Concat(\lbrace l_i^t - b_j^t \rbrace_{j=1}^9)\]Hence, the object points’ geometry representations are first enhanced as $F^t = \lbrace l_i^t , \Delta l_i^t \rbrace_{i=1}^m$. To encode the object geometry features via the proxy points, the set abstraction is adopted to aggregate the neighboring object points to every proxy point $p_k^t$ as
\[g_k^t = SetAbstraction(p_k^t, F^t), \quad for \quad k=1,\dots,K\]However, the above geometry feature encoding conducted in the local coordinate of $\lbrace B_t \rbrace_{T=1}^t$, which inevitably loses the object points’ motion information.
The per-frame motion information is also important for the object points and also needs to be properly encoded. We propose to separately calculate the relative positions between the per-frame proxy points $P^t$ and the latest proposal box’s 8 corner + 1 center points $\lbrace b_T^t \rbrace_{j=1}^9$
\[\Delta p_k^t = Concat(\lbrace p_k^t - b_j^T \rbrace_{j=1}^9)\]With an extra one-dimensional time offset embedding $e^t$, the final motion encoding of each proxy point is formulated as
\[f_k^t = MLP(Concat(\Delta p_k^t, e^t)), \quad for \quad k=1,\dots,N\]By adding the per-frame object geometry features and the motion features, the features of the each proxy point is calculated as
\[r^t_k = g^t_k + f^t_k , \quad for \quad k=1,\dots, N\]which forms the final per-frame object features $R^t = {r^t_1, \dots ,r^t_N} $at time t.
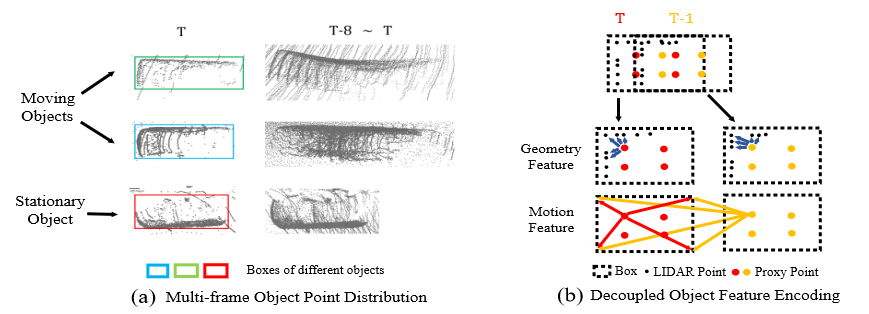
Figure. 2. Illustration of point distribution of different objects (a) and the decoupled feature encoding for object geometry and motion state (b).
Grouping for multi-frame feature interaction.
The above per-frame encoding aggregates per-frame information to the proxy points, which serve as the representations of each frame to facilitate the multi-frame feature interaction. However, naively establishing dense connections among all frames’ proxy points is still unaffordable and unscaleable in consideration of the tremendous computational costs and GPU memory. Therefore, we adopt a grouping strategy to temporally divide the long proposal trajectory into a small number of non-overlapping groups, where each group contains a short sub-trajectory.
Specifically, the trajectory’s per-frame features $\lbrace R^1,\dots, R^T \rbrace$ are evenly divided into S groups and each group has $T’$ frames (we assume that $T = T’ \times S$).
Intra-group feature mixing.
The second hierarchy aims to encode group-wise temporal features of the proposal trajectory by conducting the feature interactions within each group. We first collect the features of the inherently aligned per-frame proxy points within each group $i$ as $G^t = {r^t_1, \dots ,r^t_N}_{t \in g_i} \in R^{T’ \times N \times D}$, where $g_i$ is the temporal index set indicating which frames are included in the i-th group and $D$ is the feature dimension of each proxy point.
To further conduct the feature interaction among all proxy points within each group, inspired by [7], we propose the 3D MLP Mixer module to mix each group i’s features in the x, y, z and channel dimensions separately and sequentially. As illustrated in Fig. 1 (a), we conduct the feature interaction for each $\hat{G}^i = MLP(G^i) \in R^{N \times D}$ as
\[\hat{G}^i = MLP^{4d}(\hat{G}^i), \quad for \quad s=1,\dots, S\]where $MLP^{4d}$ indicates an MLP with four axis-aligned projection layers for feature mixing along the spatial x, y, z axes and along the channel axis (c) on the proxy points, respectively.
Inter-group feature attention.
After the intra-group feature mixing, our third hierarchy aims to propagate information of the group-level proxy points across different groups to capture richer whole-sequence information. We exploit the cross-attention per-group feature representations by querying from the features of the all-group summarization of the whole sequence.
Specifically, the all-group features $\hat{G}^1, \dots, \hat{G}^S $can be represented as a three-dimensional feature matrix denoted as $H \in R^{S\times N \times D}$. It can be considered as an $ S\times (N \times D)$ matrix and input to an MLP to obtain the all-group summarization as $\hat H = MLP(H) \in R^{N \times D}$. where the MLP(·) fuses the all-group summarization from (S × D) to D dimensions.
Using the all-group summarization as a intermediary, we conduct the intergroup cross-attention for each group $\hat{G}^i$ to aggregate features from $\hat H$ as
\[\hat{G}^i = MultiHeadAttn(Q(\hat{G}^i + PE), K(\hat H + PE), V(\hat H)), \quad for \quad s=1,\dots, S\]The above intra-group feature mixing and inter-group cross-attention are recurrently stacked for multiple times so that the trajectory’s representations gradually become aware of both global and local contexts for predicting a more accurate 3D bounding box from the trajectory proposal.
Temporal 3D Detection Head and Optimization
Through the proposed three-hierarchy feature aggregation, our model obtains richer and more reliable feature representation from input point cloud sequences. A 3D detection head to generate final bounding boxes is introduced on top of the above trajectory temporal features, which is supervised by the training losses.
3D temporal detection head with transformer.
Given the aforementioned group feature $\hat G^i$, we propose to adopt a simple transformer layer to obtain a single feature vector from each group. Specifically, we create a learnable feature embedding $E \in R^{1 \times D}$ as the query, to aggregate features from each group feature $ \hat G^i$ with a multi-head attention as
\[E^i = MultiHeadAttn(Q(E), K( \hat G^i + PE), V ( \hat G^i)), for i = 1, \dots, S\]Our detection head therefore integrates group-wise features $E^1, \dots, E^S$ from both the object points and the boxes’ embedding via feature concatenation, for the final confidence prediction and box regression.
Comments
Pros
- Solve the heterogeneity in the Number of Local Updates in Federated Learning
- Proposed a general framework which can guarantee the convergence to the stationary point.
Cons
(need further experiment)
Further work
Extending the theoretical framework to adaptive optimization methods or gossip-based training method.
Comments
(need further experiment)
References
[1] Hu, Y., Ding, Z., Ge, R., Shao, W., Huang, L., Li, K., Liu, Q.: Afdetv2: Rethinking the necessity of the second stage for object detection from point clouds. arXiv preprint arXiv:2112.09205 (2021) [2] Sun, P., Wang, W., Chai, Y., Elsayed, G., Bewley, A., Zhang, X., Sminchisescu, C., Anguelov, D.: Rsn: Range sparse net for efficient, accurate lidar 3d object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 5725–5734 (2021) [3] Yin, T., Zhou, X., Krahenbuhl, P.: Center-based 3d object detection and tracking. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. pp. 11784–11793 (2021) [4] Yang, Z., Zhou, Y., Chen, Z., Ngiam, J.: 3d-man: 3d multi-frame attention network for object detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 1863–1872 (2021) [5] Sheng, H., Cai, S., Liu, Y., Deng, B., Huang, J., Hua, X.S., Zhao, M.J.: Improving 3d object detection with channel-wise transformer. In: Proceedings of the IEEE/CVF International Conference on Computer Vision. pp. 2743–2752 (2021) [6] Shi, Shaoshuai, Xiaogang Wang, and Hongsheng Li. “Pointrcnn: 3d object proposal generation and detection from point cloud.” Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2019. [7] Tolstikhin, I.O., Houlsby, N., Kolesnikov, A., Beyer, L., Zhai, X., Unterthiner, T., Yung, J., Steiner, A., Keysers, D., Uszkoreit, J., et al.: Mlp-mixer: An all-mlp architecture for vision. Advances in Neural Information Processing Systems 34 (2021)





