Basic Information
Authors: Jianyu Wang, Qinghua Liu , Hao Liang, Gauri Joshi, H. Vincent Poor
Organization: Carnegie Mellon University, Princeton University
Source: Advances in Neural Information Processing Systems 2020
Source Code: https://github.com/JYWa/FedNova
Cite: Wang, Jianyu, et al. “Tackling the objective inconsistency problem in heterogeneous federated optimization.” Advances in neural information processing systems 33 (2020): 7611-7623.
Content
Motivation
motivation
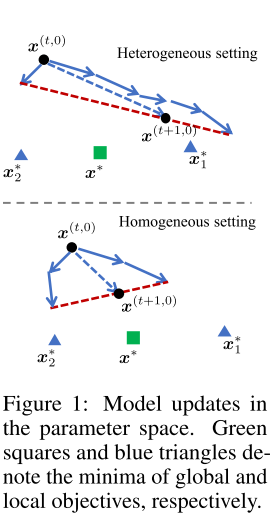
Figure 1. motivation
As we know, in federated learning, a total of \(m\) clients aim to jointly solve the following optimization problem: \(\min_x [F(x) = \sum_{i=1}^m p_i F_i(x)] \tag{1}\label1\) where \(p_i = \frac{n_i}{n}\), and \(F_i(x) = \frac{1}{n_i}\sum_{xi\in D_i}f_i(x;\xi)\)
Evaluation
Metric: Training loss, Test Accuracy
Datasets
Logistic Regression on a Synthetic Federated Dataset and DNN trained on a Non-IID partitioned CIFAR-10 dataset.
Result
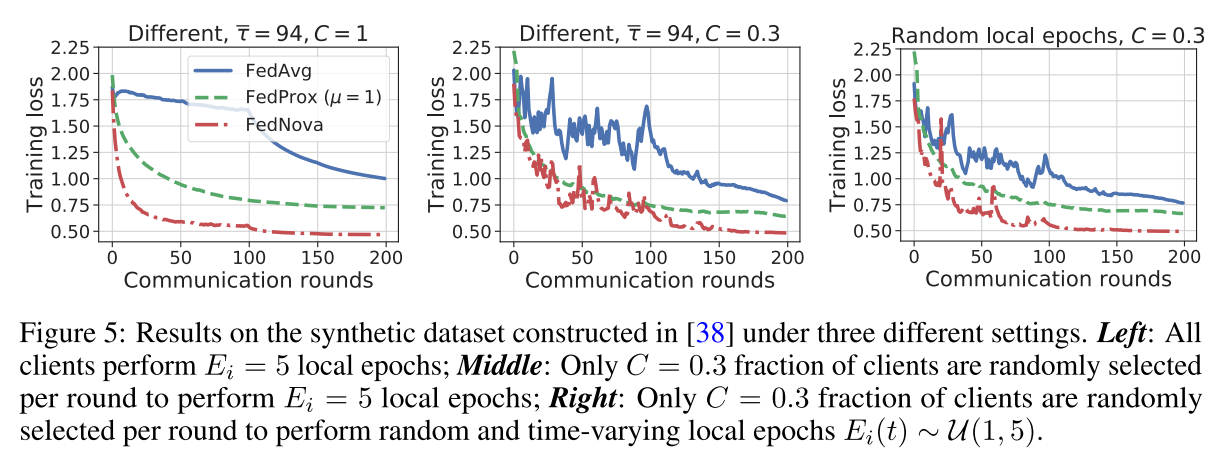
Figure 2. result
Method
The authors proposed an analysis framework to understand bias due to objective Inconsistency and proposed Federated Normalized Averaging Algorithm(FedNova) to solve this problem.
Analysis Framework
todo
Convergence Analysis
Assumption 1:(L-Smoothness) \(||\nabla F_i(x) - \nabla F_i(y)|| \le L||x-y||\)
Assumption 2:(Unbiased Gradient and Bounded Variance) \(\mathbb{E}_\xi[||g_i(x|\xi)\nabla F_i(x)||^2] \le \sigma^2 L||x-y||\)
Assumption 3:(Bounded Dissimilarity) \(\exists \beta^2\ge 0, \kappa^2\ge 0 s.t. \sum_{i=1}^{m}w_i||\nabla F_i(x)||^2 \le \beta^2||\sum_{i=1}^{m}w_i\nabla F_i(x)||^2 + \kappa^2\)
Base above assumptions, author gets following theorem:
Theorem 1(Convergence to \(\widetilde{F}(x)\) Stationary Point). Under assumptions 1 to 3, any fedrated optimizaition algorithm that follows the update rule \eqref{4}, will converge to a stationary point. if learning rate \(\eta = \sqrt{\frac{m}{\hat{\tau}T}}\), then the optimization error will be bounded as follows: \(\min_{t\in[T]} \mathbb{E}|| \nabla \widetilde{F}(x^{(t,0)})||^2 \le O(\frac{\hat{\tau}\eta}{m\tau_{eff}}) + O(\frac{A\eta\sigma^2}{m}) + O(B\eta^2\sigma^2) + O(C\eta^2\kappa^2) \tag6\) TODO
Comments
Pros
- Solve the heterogeneity in the Number of Local Updates in Federated Learning
- Proposed a general framework which can guarantee the convergence to the stationary point.
Cons
(need further experiment)
Further work
Extending the theoretical framework to adaptive optimization methods or gossip-based training method.
Comments
(need further experiment)





