Basic Information

Authors: Enmao Diao, Jie Ding, Vahid Tarokh

Organization: Duke University, University of Minnesota-Twin Cities

Source: ICLR 2021

Source Code: https://github.com/dem123456789/HeteroFL-Computation-and-Communication-Efficient-Federated-Learning-for-Heterogeneous-Clients

Cite: Diao, Enmao, Jie Ding, and Vahid Tarokh. “HeteroFL: Computation and communication efficient federated learning for heterogeneous clients.” arXiv preprint arXiv:2010.01264 (2020).

Content

Motivation

In practice, the computation and communication capabilities of each client may vary significantly and even dynamically. It is crucial to address heterogeneous clients equipped with very different computation and communication capabilities.

In this work, we propose a new federated learning framework called HeteroFL to train heterogeneous local models with varying computation complexities and still produce a single global inference model. This model heterogeneity differs significantly from the classical distributed machine learning framework where local data are trained with the same model architecture. However, to stably aggregate heterogeneous local models to a single global model under various heterogeneous settings is not apparent.

Evaluation

Metric: Accuracy

Baselines: Standalone[1], FedAvg[1], LG-FedAvg[1]

Datasets

MNIST and CIFAR10 image classification tasks and the WikiText2 language modeling task

Result

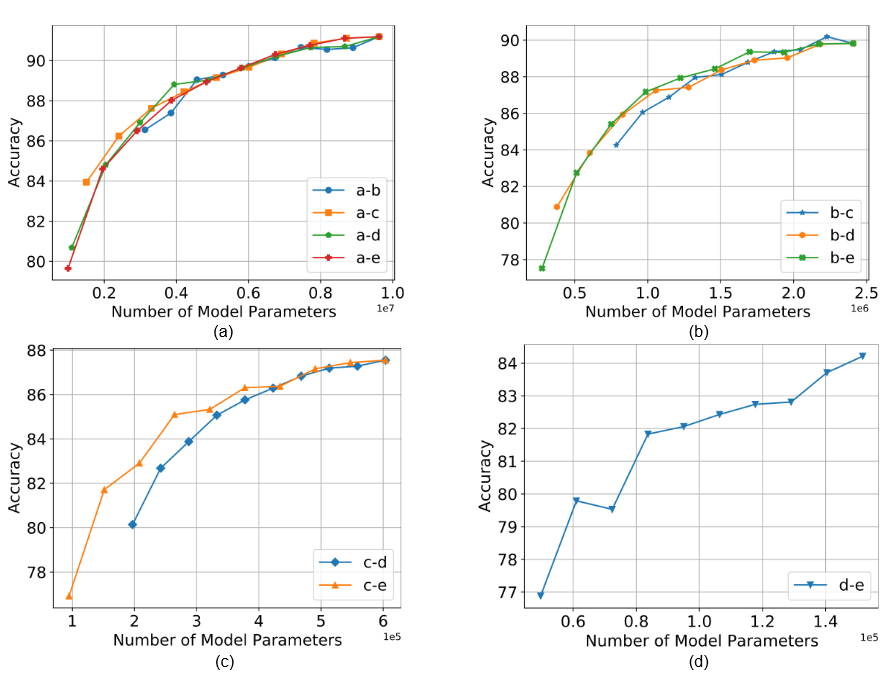
Figure 1. Interpolation experimental results for CIFAR10 (IID) dataset between global model complexity ((a) a 1, (b) b 0.5, (c) c 0.25, (d) d 0.125) and various smaller model complexities.

Method

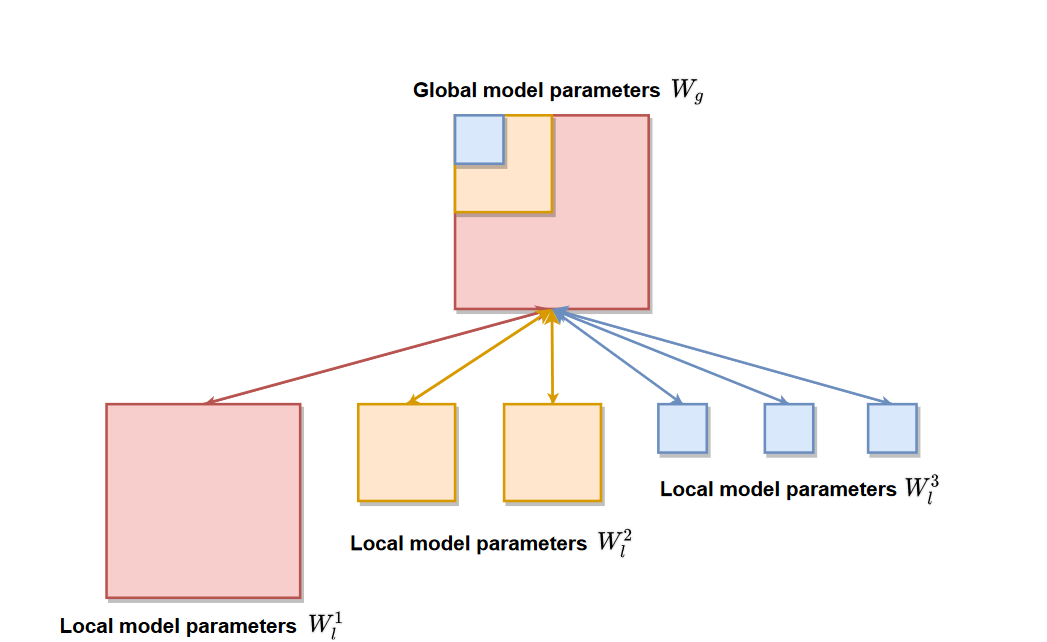
Figure 2. Global model parameters Wg are distributed to m = 6 local clients with p = 3 computation complexity levels.

Setting

Locally distributed data $\lbrace X_1, \dots, X_m \rbrace$ across $m$ clients. The local models are parameterized by model parameters $\lbrace W_1, \dots, W_m \rbrace$. The server will receive local model parameters and aggregate them into a global model $W_g$. Aggregation: $W_g^t = \frac{1}{m} \sum_{i=1}^m W_i^t$ at iteration $t$. Update local models $W_i^{t+1} = W_i^t$.

In this work, we focus on the relaxation of the assumption that local models need to share the same architecture as the global model. To simplify global aggregation and local update, it is tempting to propose local model parameters to be a subset of global model parameters $W_i^{t+1} \subset W_i^t$. However, this raises several new challenges like the optimal way to select subsets of global model parameters, compatibility of the-state-of-art model architecture, and minimum modification from the existing FL framework.

Heterogeneous models

A variety of works show that we can modulate the size of deep neural networks by varying the width and depth of networks [2, 3]. We demonstrate our method of selecting subsets of global model parameters $W_l$ for a single hidden layer parameterized by $W_g \in R^{d_g \times k_g}$ in Figure 1. where $d_g$ and $k_g$ are the output and input channel size of this layer. It is possible to have multiple computation complexity levels $W_l^p \subset W_l^{p-1} \dots \subset W_l^1$ as illustrated in Fig.1. Let $r$ be the hidden channel shrinkage ratio such that $d_l^p = r^{p-1}d_g$ and $k_l^p = r^{p-1}k_g$. It follows that the size of local model parameters $| W_l^p| = r^{2(p-1)}| W_g| $ and the model shrinkage ratio $R = \frac{| W_l^p |}{| W_g | } = r^{2(p-1)}$. Specifically, we perform global aggregation in the following way.

where $j \in [2, p]$. For notational convenience, we have dropped the iteration index $t$. We denote the $W_l^j$ as a matrix/tensor. The $W_g^t[:d_m,:k_m]$ denotes the upper left submatrix with a size of $d_m\times k_m$.

Several works show that wide neural networks can drop a tremendous number of parameters per layer and still produce acceptable results. The intuition is thus to perform global aggregation across all local models, at least on one subnetwork.

Static batch normalization

Classical FedAvg and most recent works avoid BN. A major concern of BN is that it requires running estimates of representations at every hidden layer.

We highlight an adaptation of BN named as static Batch Normaliztion (sBN) for optimizing privacy constrained heterogeneous models. During the training phase, sBN does not track running estimates and simply normalize batch data. We do not track the local running statistics as the size of local models may also vary dynamically. We also empirically found this trick significantly outperforms other forms of normalization methods including the InstanceNorm , GroupNorm , and LayerNorm.

Scaler

There still exists another cornerstone of our HeteroFL framework. Because we need to optimize local models for multiple epochs, local model parameters at different computation complexity levels will digress to various scales.

Our method directly selects subnetworks from the subsets of global model parameters. Therefore, we append a Scaler module right after the parametric layer and before the sBN and activation layers.

The Scaler module scales representations by $\frac{1}{r^{p-1}}$ during the training phase. After the global aggregation, the global model can be directly used for inference without scaling.

Comments

Pros

1. identify the possibility of model heterogeneity and propose an easy-to-implement framework HeteroFL that can train heterogeneous local models and aggregate them stably and effectively into a single global inference model.

Cons

1. BN is not learnable. Although learnable BN will produce a bad result becasue of hetergenous network architecure, I question whether simply disable it will get a better result.
2. Some parameters are trained with a lot of data but some parameters are trained with a little bit of data. I suspect whether this model is better than the small model.
3. The subnet architecure is same for clients that have same computational capablity, without considering data heterogeneity. It may cause bias.

Further work

1. We can try make the subnet architecures more diverse to train every parameters. Given every parameters have same possibility to be trained.
2. We can try to increase the relationship among local model like life-long learning, to get an optimal sub architecture.

Comments

Good paper and well written.

References

[1] Paul Pu Liang, Terrance Liu, Liu Ziyin, Ruslan Salakhutdinov, and Louis-Philippe Morency. Think locally, act globally: Federated learning with local and global representations. arXiv preprint arXiv:2001.01523, 2020.

[2] Sergey Zagoruyko and Nikos Komodakis. Wide residual networks. arXiv preprint arXiv:1605.07146, 2016.

[3] Mingxing Tan and Quoc V Le. Efficientnet: Rethinking model scaling for convolutional neural networks. arXiv preprint arXiv:1905.11946, 2019.