Basic Information

Authors: Horvath, Samuel, Stefanos Laskaridis, Mario Almeida, Ilias Leontiadis, Stylianos Venieris, and Nicholas Lane.

Organization: Samsung AI Center, KAUST

Source: NeurIPS 2021

Source Code: None

Cite: Horvath, Samuel, et al. “Fjord: Fair and accurate federated learning under heterogeneous targets with ordered dropout.” Advances in Neural Information Processing Systems 34 (2021): 12876-12889.

Content

Motivation

A key challenge of deploying FL in the wild is the vast heterogeneity of devices, ranging from low-end IoT to flagship mobile devices. Despite this fact, the widely accepted norm in FL is that the local models have to share the same architecture as the global model. Under this assumption, developers typically opt to either drop low-tier devices from training, hence introducing training bias due to unseen data, or limit the global model’s size to accommodate the slowest clients, leading to degraded accuracy due to the restricted model capacity.

In this work, we introduce FjORD, a novel adaptive training framework that enables heterogeneous devices to participate in FL by dynamically adapting model size – and thus computation, memory and data exchange sizes – to the available client resources. To this end, we introduce Ordered Dropout (OD), a mechanism for run-time ordered (importance-based) pruning, which enables us to extract and train submodels in a nested manner. As such, OD enables all devices to participate in the FL process independently of their capabilities by training a submodel of the original DNN, while still contributing knowledge to the global model. Alongside OD, we propose a self-distillation method from the maximal supported submodel on a device to enhance the feature extraction of smaller submodels. Finally, our framework has the additional benefit of producing models that can be dynamically scaled during inference, based on the hardware and load constraints of the device.

Evaluation

Metric: Accuracy, MACs

Datasets

CIFAR10, FEMNIST, Shakespeare, IID version

Result

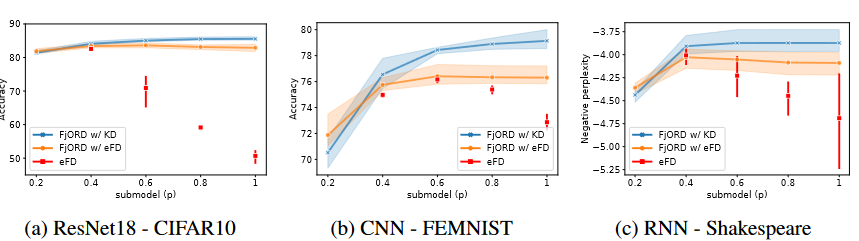
Figure 1. Ordered Dropout with KD vs eFD baselines. Performance vs dropout rate p across different networks and datasets. $D_P = U_5$

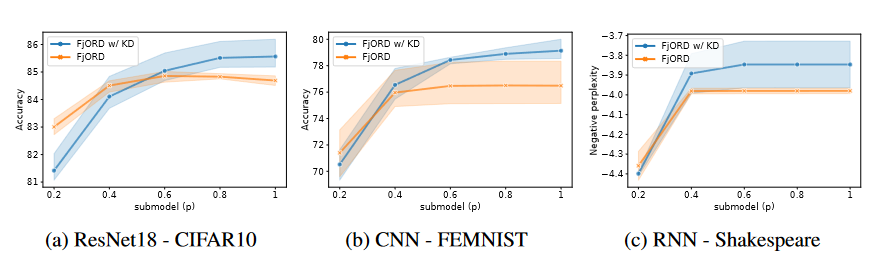
Figure 2. Ablation analysis of FjORD with Knowledge Distillation. Ordered Dropout with $D_P = U_5$, KD - Knowledge distillation.

Method

We have devised a mechanism of importance-based pruning for the easy extraction of subnetworks from the original, specially trained model, each with a different computational and memory footprint. We name this technique Ordered Dropout (OD), as it orders knowledge representation in nested submodels of the original network, As shown in Figure 3.

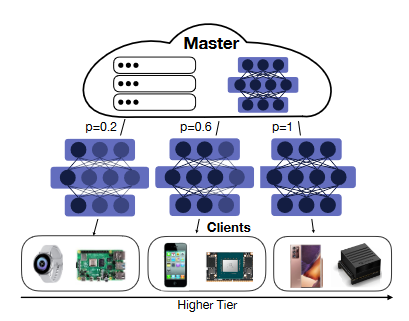
Figure 3. FjORD employs OD to tailor the amount of computation to the capabilities of each participating device.

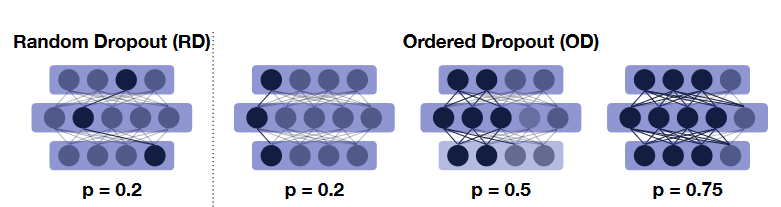
Figure 4. Ordered vs. Random Dropout. In this example, the left-most features are used by more devices during training, creating a natural ordering to the importance of these features.

More specifically, our technique starts by sampling a value (denoted by p) from a distribution of candidate values. Each of these values corresponds to a specific submodel, which in turn gets translated to a specific computational and memory footprint. Such sampled values and associations are depicted in Fig. 2. Contrary to conventional dropout (RD), our technique drops adjacent components of the model instead of random neurons, which translates to computational benefits in today’s linear algebra libraries and higher accuracy as shown later.

Ordered Dropout Mechanics

The proposed OD method is parametrised with respect to: i) the value of the dropout rate $p \in (0,1]$ per layer, ii) the set of candidate values P, such that $p \in P$ and iii) the sampling method of p over the set of candidate values, such that $p \sim D_p$ where $D_p$ is the distribution over P.

Given a $p$ value, a pruned p-subnetwork can be directly obtained as follows. For each layer $l$ with width $K_l$, the submodel for a given p has all neurons/filters with index $\lbrace 0, 1, \dots, [p\cdot K_l] - 1 \rbrace$ included and $\rbrace 0, 1, \dots, [p\cdot K_l] - 1 \lbrace$ pruned. Moreover, the unnecessary connections between pruned neurons/filters are also removed. We denote a pruned p-subnetwork $F_p$ with its weights $w_p$, where $F$ and $w$ are the original network and weights, respectively.

Training OD Formulation

We propose two ways to train an OD-enabled network: i) plain OD and ii) knowledge distillation OD training (OD w/ KD).

In the first approach, in each step we first sample $p \sim D_p$ ; then we perform the forward and backward pass using the p-reduced network $F_p$; finally we update the submodel’s weights using the selected optimiser.

In the second approach we exploit the nested structure of OD, i.e. $p_1 \le p_2 \rightarrow F_{p_1} \subset F_{p_2}$ and allow for the bigger capacity supermodel to teach the sampled p-reduced network at each iteration via knowledge distillation (teacher $p_{max} > p, p_{max} = max P$). In particular, in each iteration, the loss function consists of two components as follows:

where $SM_p$ is the softmax output of the sampled p-submodel, $y_{label}$ is the ground-truth label, $CE$ is the cross-entropy function, $KL$ is the KL divergence, $T$ is the distillation temperature, and $\alpha$ is the relative weight of the two components. We observed in our experiments always backpropagating also the teacher network further boosts performance. Furthermore, the best performing values for distillation were α = T = 1, thus smaller models exactly mimic the teacher output. This means that new knowledge propagates in submodels by proxy. (question: where to run the $SM_{p_{max}}$ ? )

Ordered Dropout exactly recovers SVD

We further show that our new OD formulation can recover the Singular Value Decomposition (SVD) in the case where there exists a linear mapping from features to responses. We formalise this claim in the following theorem.

TODO

FjORD

Building upon the shoulders of OD, we introduce FjORD, a framework for federated training over heterogenous clients. We subsequently describe the FjORD’s workflow, further documented in Alg. 1.

Subnetwork Knowledge Transfer. We extend this approach to FjORD, where instead of the full network, we employ width $max \rbrace p \in P: p \le p_{max}^i \rbrace$ as a teacher network in each local iteration on device i. We provide the alternative of FjORD with knowledge distillation mainly as a solution for cases where the client bottleneck is memory- or network-related, rather than computational in nature. However, in cases where client devices are computationally bound in terms of training latency, we propose FjORD without KD or decreasing pimax to account for the overhead of KD.

Comments

Pros

I found this paper to be quite good.

1. Initially, I was unsure if applying order to dropout was necessary. However, the paper convinced me that ordered dropout can make the model faster while also suffering lower accuracy decreasing.
2. The explanation of ordered dropout in the context of SVD was particularly impressive and reasonable.
3. Self-KD makes sense.

Cons

1. This idea of ordered pruning can induce bias in gradients, especially if clusters are imbalanced.

Further work

1. Non-IID data distribution

Comments

(need further experiment)

References