Basic Information

Authors: Yifan Lu, Quanhao Li, Baoan Liu, Mehrdad Dianati, Chen Feng, Siheng Chen, Yanfeng Wang

Organization: Shanghai Jiao Tong University, Nanjing University,

Source: ICRA 2023

Source Code: https://github.com/yifanlu0227/CoAlign

Cite: Lu, Yifan, et al. “Robust Collaborative 3D Object Detection in Presence of Pose Errors.” arXiv preprint arXiv:2211.07214 (2022).

Content

Motivation

To share valid information with each other, multiple agents need precise poses to synchronize their individual data in a consistent spatial coordinate system, which is a foundation of the collaboration. However, the 6 DoF pose estimated by each agent’s localization module is not perfect in practice, causing annoying relative pose noises. Such relative pose noises would fundamentally reduce the collaboration quality. To address this issue, previous works consider various methods to promote pose robustness. However, these methods require the ground-truth poses in training data. Although pose noises in training data could be corrected offline, this labeling process could be expensive and imperfect.

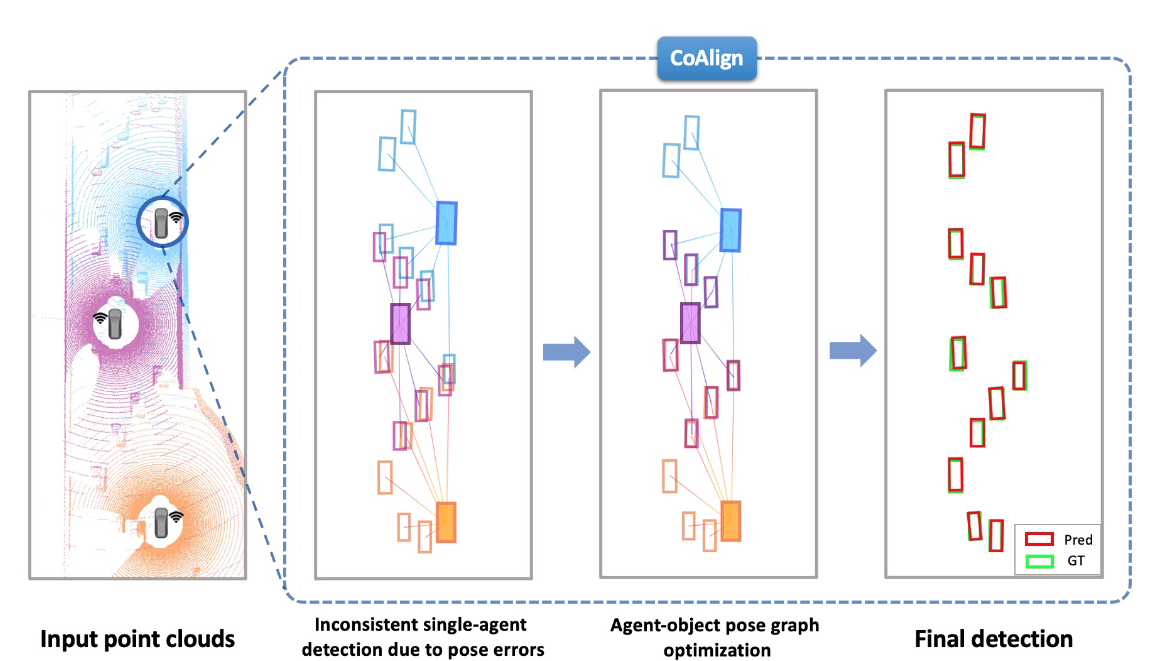
Figure 1. Based on agent-object pose graph optimization, our CoAlign reduces relative pose errors and improves detection robustness.

Motivated by this limitation, we propose a novel hybrid collaboration framework CoAlign, which enables multiple agents to share both intermediate features and single-agent detection results. CoAlign can handle arbitrary pose errors without any accurate pose supervision in the training phase. To realize this, the core idea is to leverage novel agent-object pose graph optimization to align the relative pose relations between agents and detected objects in the scene, promoting pose consistency. Here, pose consistency means that the poses of an object should be consistent from multiple agents’ perspectives. To effectively alleviate the impact of pose error, we further consider a multiscale intermediate fusion strategy, which comprehensively aggregates collaboration information at multiple spatial scales.

Evaluation

Metric: AP@0.5 AP@0.7

Baselines: F-Cooper, V2VNet, DiscoNet, OPV2V, MASH, FPV-RCNN, V2VNet(robust), V2X-ViT.

Datasets

V2X-Sim 2.0, OPV2V, DAIR-V2X

Result

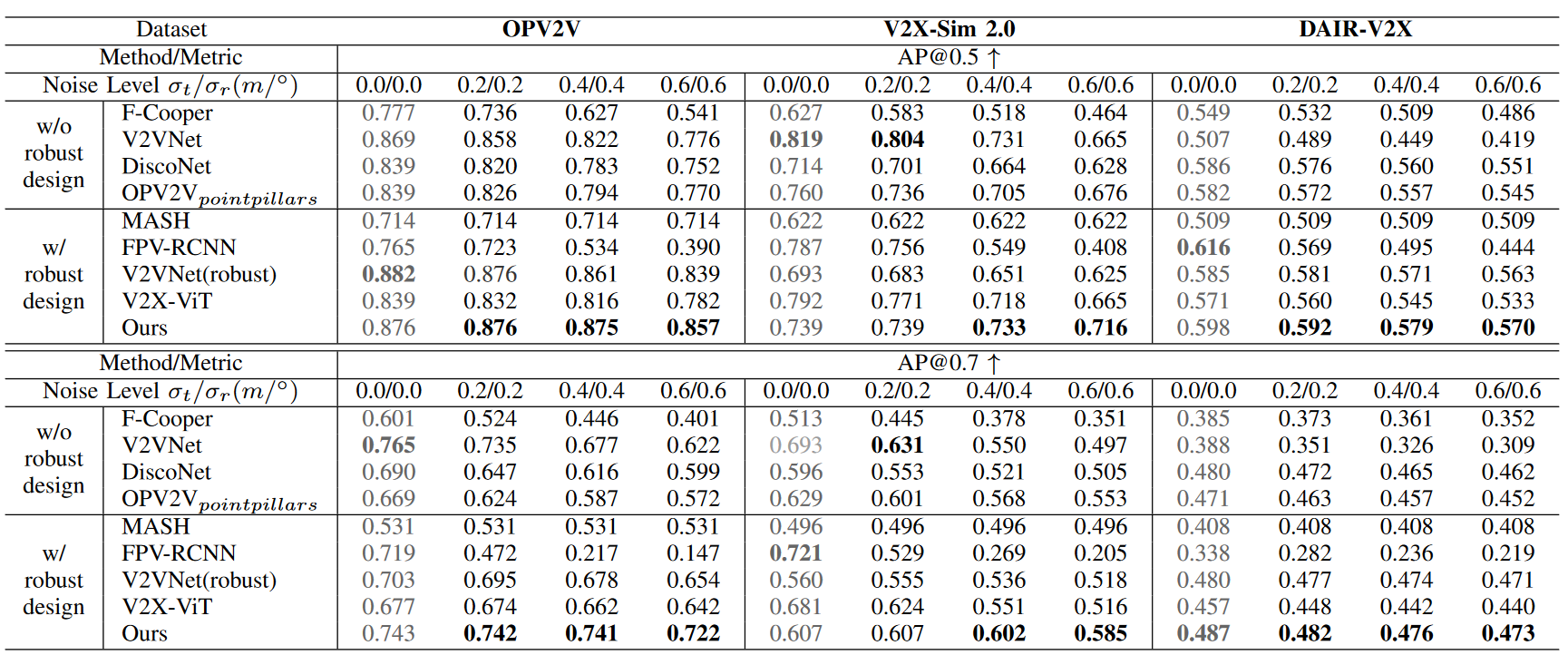
Table 1. Detection performance on OPV2V, V2X-Sim 2.0 and DAIR-V2X datasets with pose noises following Gaussian distribution in the testing phase. All models are trained on pose noises following Gaussian distribution with $\delta_t= 0.2m$ , $\delta_r= 0.2$. Experiments show that CoAlign holds the best resistance to localization error under various noise levels.

Method

Problem Formulation

Consider $N$ agents in the scene. Let $O_i$ and $B_i$ be the perceptual observation and the detection output of the ith agent, respectively. For the ith agent, a standard 3D object detection based on intermediate collaboration works as follows:

where $F_i$ is the feature extracted from the ith agent’s observation, $\xi_i = \lbrace x_i, y_i, z_i, \theta_i, \phi_i, \psi_i \rbrace$ is the 6DoF pose of the $i$th agent with $\theta_i, \phi_i, \psi_i$ the yaw, pitch and roll angle, $ M_{j \rightarrow i} $ is the message transmitted from the $j$th agent to the $i$th agent, whose coordinate space is aligned with $F_i$ through pose transformation, and $F’_i$ is the aggregated feature of the $i$th agent after fusing other agents’ messages. Note that: i) before pose transformation, the direct message transmitted from the $j$th agent to the ith agent is $(F_j, \xi_j)$, , including both the feature and the pose; and ii) single-agent detection only considers Steps (1a) and (1d) with $F’_i = F_i$.

In practice, each 6DoF pose $\xi_i$ is estimated by the localization module in real time, which is always noisy. Then, after pose transformation in Step (1b), each message $M_{j \rightarrow i}$ would have different intrinsic coordinate systems, resulting in fusion misalignment in Step (1c) and unsatisfying detection output in Step (1d). The goal of this work is to minimize the effect of pose errors by introducing additional pose correction before Step (1b).

Pose-Robust collaborative 3D detection

Now we propose CoAlign, a novel hybrid collaboration framework, which combines intermediate and late collaboration, transmitting both intermediate features and the detection output. Compared with intermediate collaboration, this hybrid collaboration can leverage those bounding boxes detected by agents to be the scene landmarks and correct the relative poses between agents. Mathematically, for the $i$th agent, the proposed CoAlign works as:

where $B_i$ and $B_i’$ are the detection outputs before and after collaboration, respectively, and $\xi_{j\leftarrow i}’ $ is the corrected relative pose from ith agent’s perspective to jth agent ($\xi_{i\leftarrow i}’ is the identity). Step (2a) is similar to Step (1a), while Step (2a) completes the detection by a single agent and further outputs the detected boxes, which will be elaborated in Section IV-B. As the key step, Step (2b) corrects the relative pose based on all the noisy poses and detected boxes obtained from the other agents; will see details in Section IV-C. Step (2c) synchronizes other agents’ features to the ego pose based on the corrected relative pose. To further ensure the robustness towards pose noises, Step (2d) uses a robust multiscale fusion to update the feature, where $M_{i \leftarrow i} = F_i$. Finally, Step (2e) uses fused features to obtain final detections; also see the illustration of the overall architecture in Figure 2.

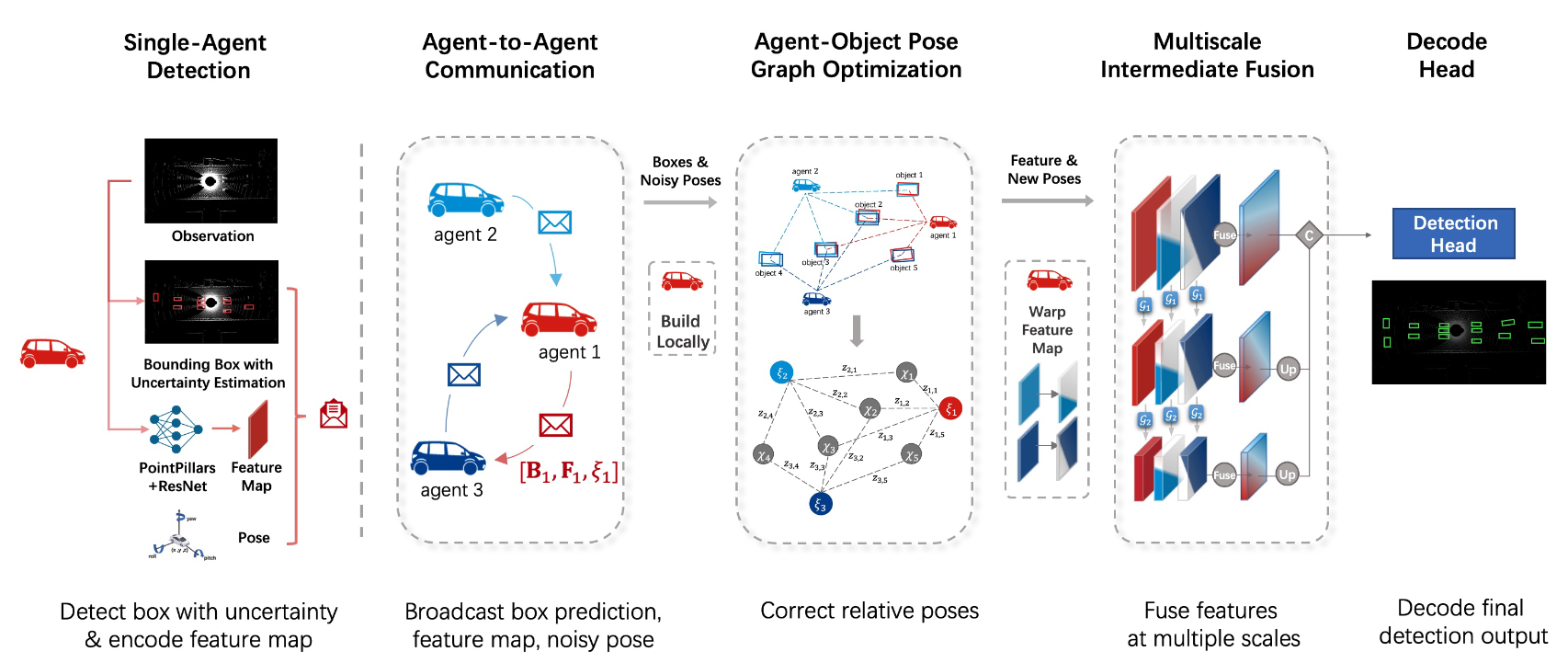
Figure 2. Overview of CoAlign. Before communication, each agent uses input raw observation to i) predict the bounding box with uncertainty estimation ii) generate intermediate features. Agents pack i) and ii) with measured poses and broadcast to other agents. By aggregating incoming messages, each agent builds the agent-object pose graph and locally optimizes relative poses. Corrected poses are utilized for warping feature maps to the ego coordinate, which goes through a multiscale intermediate fusion module afterward. Finally, fused features are decoded into the final detection output.

Agent-Object Pose Graph Optimization

To reliably fuse feature maps from other agents, each agent needs to correct the relative poses. To achieve this, the core idea is to align the corresponding bounding boxes of the same object, which are detected by multiple agents. We thus leverage an agent-object pose graph to represent the relations between agents and objects; and then, apply optimization over this graph to achieve pose alignment. Concretely, the ith agent receives the messages from all the other agents and builds its internal agent-object pose graph $G(V^{(agent)}, V^{(object)}, E)$, which is a bipartite graph to model the relations between agents and detected objects. The node set $V^{(agent)}$ consists of all the N agents, the node set $V^{(object)}$ includes all the unique objects, which are obtained via spatially clustering similar boxes received from all the agents, and the edge set E reflects the detection relationship between agents and objects: when an agent detects a bounding box on an object, we set an edge connecting them. Notably, this agent-object pose graph is built locally at each agent, but it is the same for all the agents.

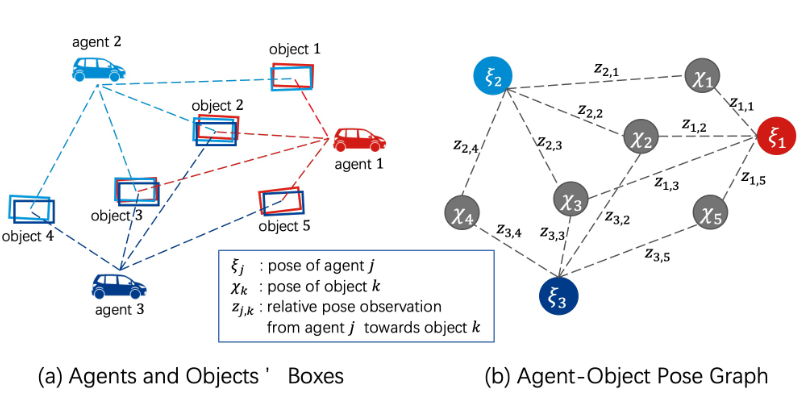
Figure 3. Agent-object pose graph illustration.

In this agent-object pose graph, each node is associated with a pose. For the jth agent in the scene, its pose $\xi_j$ is estimated by its localization module; for the $k$th object in the scene, its pose $\chi_{k}$ is sampled from multiple bounding boxes in the same box cluster, which is essentially the unique object detected by multiple agents. Correspondingly, each edge in E reflects a relative pose between an agent and an object. Let be the $z_{j k}=(\hat{x},\hat y,\hat\theta)$ relative pose of the kth object from the perspective of the jth agent, which is naturally obtained through the jth agent’s detection output. Ideally, the pose of an object should be consistent from the views of multiple agents; that is, the pose consistency error vector $e_{jk}=z_{ik}^{-1}\circ(\xi_{j}^{-1}\circ\chi_{k})\in\mathbb{R}^{3}$ should be zero, where $\circ$ is motion composition operator, equivalent to multiplying their corresponding homogeneous transformation matrices. We denote $\xi^{-1}$ as the inverse pose, equivalent to inverting the corresponding transformation matrix.

To promote this pose consistency, we consider the following optimization problem

where $\Omega_{jk} = diag([1/\delta_x^2, 1/\delta_y^2, 1/\delta_\theta^2]) \in R ^{3 \times 3}$ is analog to information matrix in graph-based SLAM, gauging how we are confident in this measurement. The diagonal elements are from box’s uncertainty estimation.

Comments

Pros

1. The proposed agentobject pose graph optimization empowers CoAlign to handle arbitrary pose errors without any accurate pose supervision.

Cons

1. computational cost

Further work

(need further experiment)

Comments

(need further experiment)

References