BEVFormer Learning Bird’s-Eye-View Representation from Multi-Camera Images via Spatiotemporal Transformers

2023-02-03

Basic Information

Authors: Zhiqi Li, Wenhai Wang, Hongyang Li, Enze Xie, Chonghao Sima, Tong Lu, Yu Qiao, Jifeng Dai

Organization: Nanjing University, Shanghai AI Laboratory, The University of Hong Kong

Source: ECCV 2022

Source Code: https://github.com/fundamentalvision/BEVFormer

Cite: Li, Zhiqi, et al. “Bevformer: Learning bird’s-eye-view representation from multi-camera images via spatiotemporal transformers.” Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part IX. Cham: Springer Nature Switzerland, 2022.

Content

Motivation

3D object detection task requires strong BEV features to support accurate 3D bounding box prediction, but generating BEV from the 2D planes is ill-posed. A popular BEV framework that generates BEV features is based on depth information, but this paradigm is sensitive to the accuracy of depth values or the depth distributions. The detection performance of BEV-based methods is thus subject to compounding errors, and inaccurate BEV features can seriously hurt the final performance.

Therefore, we are motivated to design a BEV generating method that does not rely on depth information and can learn BEV features adaptively rather than strictly rely on 3D prior.

The existing state-of-the-art multi-camera 3D detection methods rarely exploit temporal information. The significant challenges are that autonomous driving is time-critical and objects in the scene change rapidly, and thus simply stacking BEV features of cross timestamps brings extra computational cost and interference information, which might not be ideal. Inspired by recurrent neural networks (RNNs), we utilize the BEV features to deliver temporal information from past to present recurrently, which has the same spirit as the hidden states of RNN models.

As shown in Fig. 1, we present a transformer-based bird’s-eye-view (BEV) encoder, termed BEVFormer, which can effectively aggregate spatiotemporal features from multi-view cameras and history BEV features.

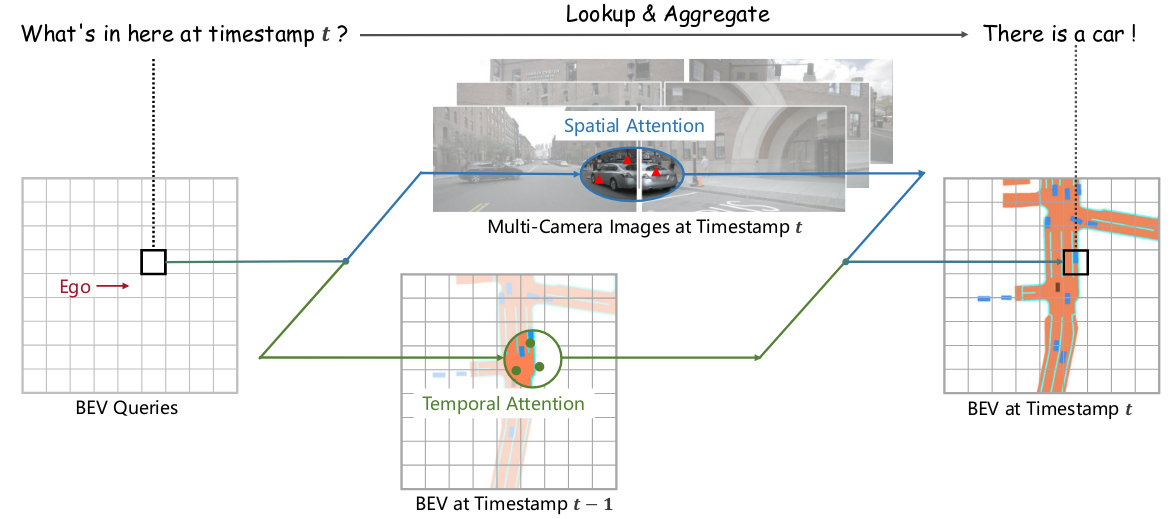
Figure 1. We propose BEVFormer, a paradigm for autonomous driving that applies both Transformer and Temporal structure to generate bird’s-eye-view (BEV) features from multi-camera inputs. BEVFormer leverages queries to lookup spatial/temporal space and aggregate spatiotemporal information correspondingly, hence benefiting stronger representations for perception tasks.

Evaluation

Metric. Nuscenes Metrics(NDS, AP, ATE, ASE, AOE) and Waymo Metrics(AP@IoU 0.5 and 0.7) **Baselines. ** To eliminate the effect of task heads and compare other BEV generating methods fairly, we use VPN [30] and Lift-Splat [32] to replace our BEVFormer and keep task heads and other settings the same.

Datasets

nuScenes and Waymo

Result

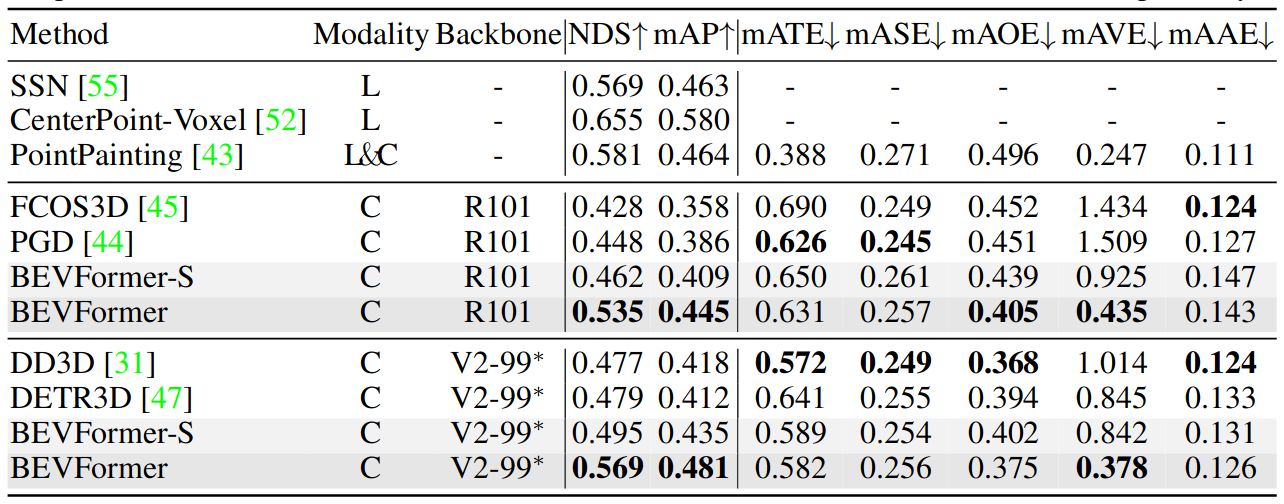
Table 1. 3D detection results on nuScenes test set. ∗ notes that VoVNet-99 (V2-99) was pre-trained on the depth estimation task with extra data. “BEVFormer-S” does not leverage temporal information in the BEV encoder. “L” and “C” indicate LiDAR and Camera, respectively.

Method

We present a new transformer-based framework for BEV generation, which can effectively aggregate spatiotemporal features from multi-view cameras and history BEV features via attention mechanisms.

Overall Architecture

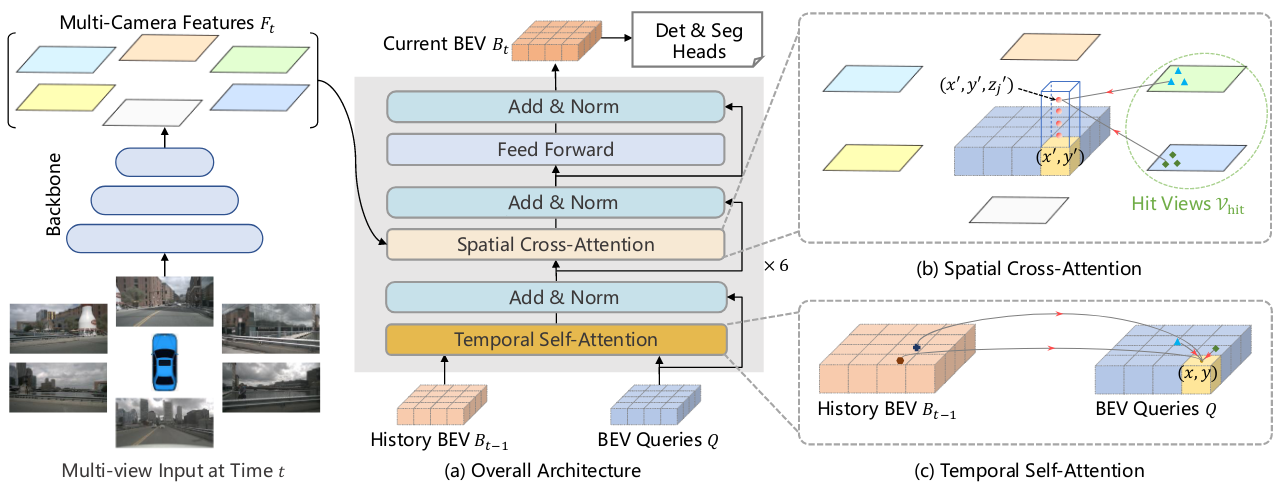
Figure 2. Overall architecture of BEVFormer. (a) The encoder layer of BEVFormer contains grid-shaped BEV queries, temporal self-attention, and spatial cross-attention. (b) In spatial crossattention, each BEV query only interacts with image features in the regions of interest. (c) In temporal self-attention, each BEV query interacts with two features: the BEV queries at the current timestamp and the BEV features at the previous timestamp.

As illustrated in Fig. 2, BEVFormer has 6 encoder layers, each of which follows the conventional structure of transformers, except for three tailored designs, namely BEV queries, spatial crossattention, and temporal self-attention.

During inference, at timestamp $t$, we feed multi-camera images to the backbone network and obtain the features $F_t=\lbrace F_t^i\rbrace_{i=1}^{N_{view}} $ of different camera views, where $F_t^i$ is the feature of the $i$-th view, $N_{view}$ is the total number of camera views. At the same time, we preserved the BEV features $B_{t-1}$ at the prior timestamp $t-1$. In each encoder layer, we first use BEV queries $Q$ to query the temporal information from the prior BEV features $B_{t−1}$ via the temporal self-attention.

After the feed-forward network, the encoder layer output the refined BEV features, which is the input of the next encoder layer. After 6 stacking encoder layers, unified BEV features Bt at current timestamp $t$ are generated. Taking the BEV features $B_t$ as input, the 3D detection head and map segmentation head predict the perception results such as 3D bounding boxes and semantic map.

BEV Queries

We predefine a group of grid-shaped learnable parameters $Q \in R^{H\times W \times C} $ as the queries of BEVFormer, where H, W are the spatial shape of the BEV plane. To be specific, the query $Q_p \in R^{1\times C}$ located at $p = (x, y)$ of $Q$ is responsible for the corresponding grid cell region in the BEV plane. Each grid cell in the BEV plane corresponds to a real-world size of $s$ meters. The center of BEV features corresponds to the position of the ego car by default.

Spatial Cross-Attention

Due to the large input scale of multi-camera 3D perception (containing $N_{view}$ camera views), the computational cost of vanilla multi-head attention is extremely high. Therefore, we develop the spatial cross-attention based on deformable attention, which is a resource-efficient attention layer where each BEV query $Q_p$ only interacts with its regions of interest across camera views.

As shown in Fig. 2 (b), we first lift each query on the BEV plane to a pillar-like query, sample $N_{ref}$ 3D reference points from the pillar, and then project these points to 2D views. For one BEV query, the projected 2D points can only fall on some views, and other views are not hit. Here, we term the hit views as $V_{hit}$. After that, we regard these 2D points as the reference points of the query Qp and sample the features from the hit views $V_{hit}$ around these reference points.Finally, we perform a weighted sum of the sampled features as the output of spatial cross-attention. The process of spatial cross-attention (SCA) can be formulated as:

\[SCA(Q_p, F_t) = \frac{1}{|V_{hit}|} \sum_{i\in V_{hit}} \sum_{j=1}^{N_{ref}} DeformAttn(Q_p, P(p,i,j), F_{t}^i),\]

where $i$ indexes the camera view, $j$ indexes the reference points, and $N_{ref}$ is the total reference points for each BEV query. $F_t^i$ is the features of the $i$-th camera view. For each BEV query $Q_p$, we use a project function $P(p, i, j)$ to get the $j$-th reference point on the $i$-th view image.

Next, we introduce how to obtain the reference points on the view image from the projection function $P$. We first calculate the real world location $(x′, y′)$ corresponding to the query $Q_p$ located at $p = (x, y)$ of Q as:

\[x^{\prime}=(x-{\frac{W}{2}})\times s;\quad y^{\prime}=(y-{\frac{H}{2}})\times s,\]

where $H, W$ are the spatial shape of BEV queries, $s$ is the size of resolution of BEV’s grids, and $(x′, y′)$ are the coordinates where the position of ego car is the origin.

We predefine a set of anchor heights $\lbrace z_{j}^{\prime} \rbrace_{j=1}^{N_{\mathrm{ref}}^{\prime}}$ to make sure we can capture clues that appeared at different heights. In this way, for each query $Q_p$, we obtain a pillar of 3D reference points $(x’,y’,z_j’)^{N_{ref}}_{j=1} $ inally, we project the 3D reference points to different image views through the projection matrix of cameras, which can be written as:

\[P(p, i, j) = (x_{ij}, y_{ij})\]

where

\[z_{ij} \cdot [x_{ij}, y_{ij};1]^T = T_i\cdot [x';y';z_j';1]^T\]

Here, $P(p, i, j)$ is the 2D point on i-th view projected from j-th 3D point $(x′, y′, z′_j ), T_i \in R^{3×4}$ is the known projection matrix of the $i$-th camera.

Temporal Self-Attention

In addition to spatial information, temporal information is also crucial for the visual system to understand the surrounding environment. Given the BEV queries $Q$ at current timestamp $t$ and history BEV features $B_{t−1}$ preserved at timestamp $t−1$, we first align $B_{t−1}$ to $Q$ according to ego-motion to make the features at the same grid correspond to the same real-world location. Here, we denote the aligned history BEV features $B_{t−1}$ as $B’_{t−1}$. However, from times t − 1 to t, movable objects travel in the real world with various offsets. It is challenging to construct the precise association of the same objects between the BEV features of different times. Therefore, we model this temporal connection between features through the temporal self-attention (TSA) layer, which can be written as follows:

\[\mathrm{TSA}(Q_{p},\{Q,B_{t-1}^{\prime}\})=\sum_{V\in\{Q,B_{t-1}^{\prime}\}}\mathrm{DeformAttn}(Q_{p},p,V),\]

where $Q_p$ denotes the BEV query located at $p = (x, y)$. In addition, different from the vanilla deformable attention, the offsets $\Delta p$ in temporal self-attention are predicted by the concatenation of $Q$ and $B_{t−1}’$. Specially, for the first sample of each sequence, the temporal self-attention will degenerate into a self-attention without temporal information, where we replace the BEV features $\lbrace Q, B’_{t-1} \rbrace$ with duplicate BEV queries $\lbrace Q, Q \rbrace$.