Where2comm Communication-Efficient Collaborative Perception via Spatial Confidence Maps

2023-01-27

Basic Information

Authors: Yue Hu; Shaoheng Fang; Zixing Lei; Yiqi Zhong; Siheng Chen

Organization: Shanghai Jiao Tong University; University of Southern California

Source: 36th Conference on Neural Information Processing Systems (NeurIPS 2022)

Source Code: https://github.com/MediaBrain-SJTU/where2comm

Content

Motivation

Recent methods in multi-agent collaborative perception are obligated to share perceptual information of all spatial areas equally. This unnecessary assumption can hugely waste the bandwidth as a large proportion of spatial areas may contain irrelevant information for perception task. Figure 1 illustrates such a spatial heterogeneity of perceptual information.

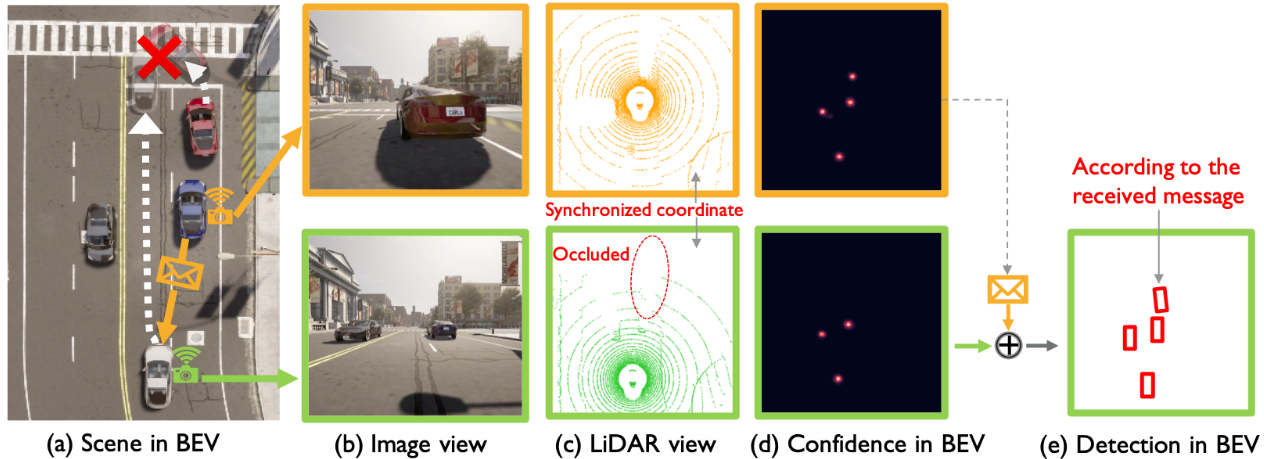
Figure 1. Collaborative perception could contribute to safety-critical scenarios, where the white car and the red car may collide due to occlusion. This collision could be avoided when the blue car can share a message about the red car’s position. Such a message is spatially sparse, yet perceptually critical. Considering the precious communication bandwidth, each agent needs to speak to the point!

To fill this gap, we consider a novel spatial-confidence-aware communication strategy. The core idea is to enable a spatial confidence map for each agent, where each element reflects the perceptually critical level of a corresponding spatial area. Based on this map, agents decide which spatial area (where) to communicate about. That is, each agent offers spatially sparse, yet critical features to support other agents, and meanwhile requests complementary information from others through multi-round communication to perform efficient and mutually beneficial collaboration.

Evaluation

**Metric: **The detection results are evaluated by Average Precision (AP) at Intersection-over-Union (IoU) threshold of 0.50 and 0.70.

Experiments details: The communication results count the message size by byte in log scale with base 2. To compare communication results straightforward and fair, we do not consider any extra data/feature/model compression.

Baselines: When2com, V2VNet, DiscoNet, V2X-ViT and late fusion.

Datasets

OPV2V, V2X-Sim, CoPerception-UAVs and DAIR-V2X.

Result

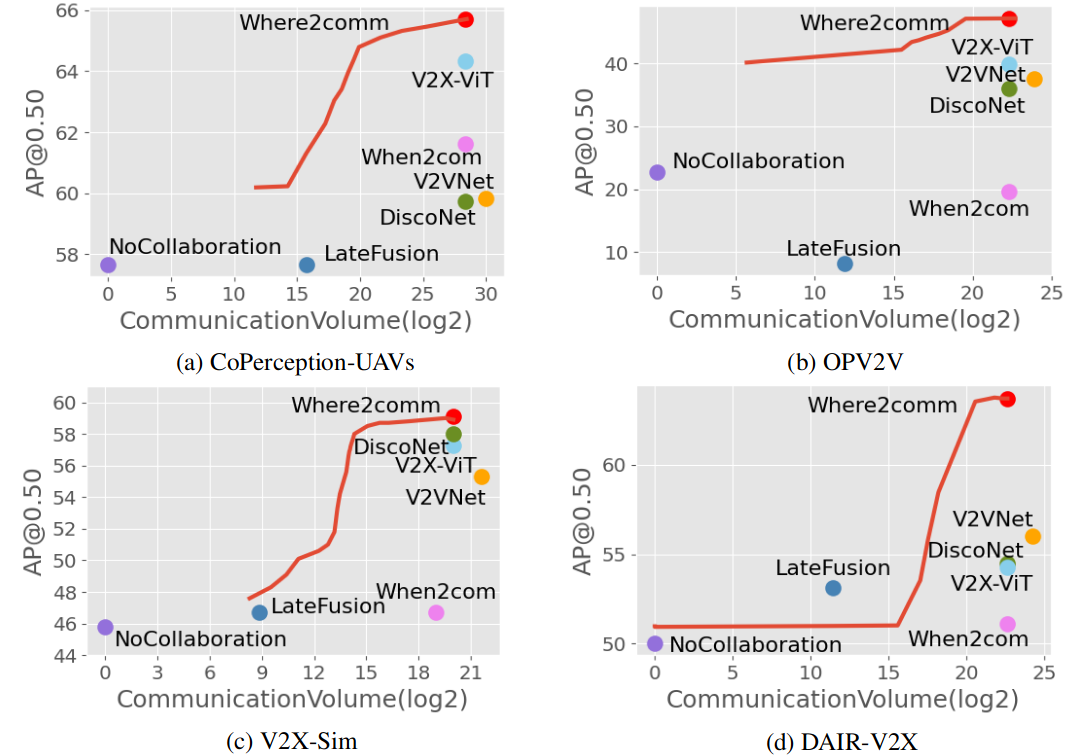
Figure 2. Where2comm achieves consistently superior performance-bandwidth trade-off on all the three collaborative perception datasets, e.g, Where2comm achieves 5,000 times less communication volume and still outperforms When2com on CoPerception-UAVs dataset. The entire red curve comes from a single Where2comm model evaluated at varying bandwidths.

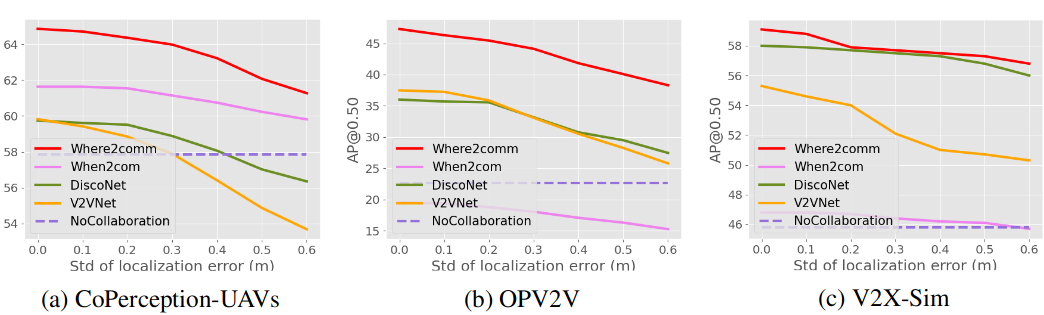
Figure 3. Robustness to localization error. Gaussian noise with zero mean and varying std is introduced. Where2comm consistently outperforms previous SOTAs and No Collaboration.

Method

See the overview in Fig. 4. Where2comm includes an observation encoder, a spatial confidence generator, the spatial confidence-aware communication module, the spatial confidence-aware message fusion module and a detection decoder.

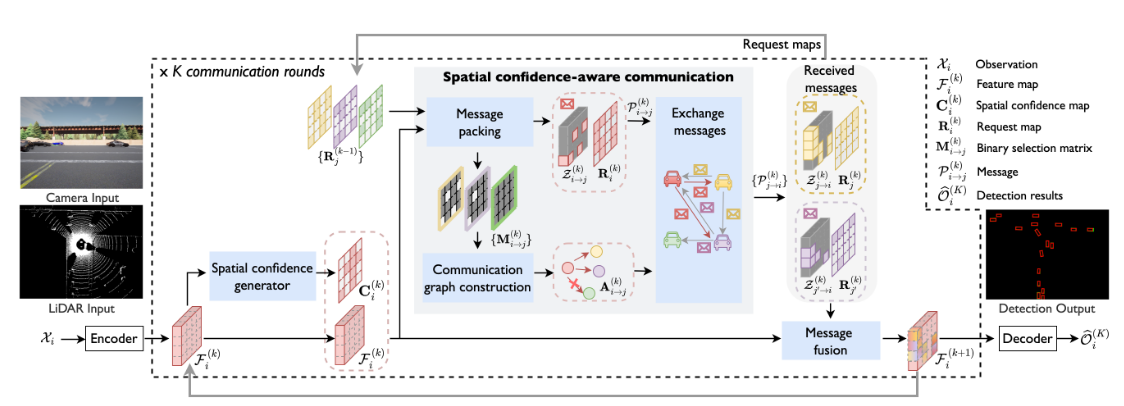
Figure 4. System overview. In Where2comm, spatial confidence generator enables the awareness of spatial heterogeneous of perceptual information, spatial confidence-aware communication enables efficient communication, and spatial confidence-aware message fusion boosts the performance.

Observation encoder

The observation encoder extracts feature maps from the sensor data. Where2comm accepts single/multimodality inputs, such as RGB images and 3D point clouds. This work adopts the feature representations in bird’s eye view (BEV), where all agents project their individual perceptual information to the same global coordinate system, avoiding complex coordinate transformations and supporting better shared cross-agent collaboration.

For the $i$th agent, given its input $X_i$, the feature map is $F_i^{(0)} = \Phi_{enc}(X_i) \in R^{H \times W \times C}$, where $\Phi_{enc}(\cdot)$ is the encoder,the superscript $0$ reflects that the feature is obtained before communication. For the image input, $\Phi_{enc}(\cdot)$ is followed by a warping function that transforms the extracted feature from front-view to BEV. For 3D point cloud input, we discretize 3D points as a BEV map and $\Phi_{enc}(\cdot)$ extracts features in BEV. The extracted feature map is output to the spatial confidence generator and the message fusion module.

Spatial confidence generator

The spatial confidence generator generates a spatial confidence map from the feature map of each agent. we represent the spatial confidence map with the detection confidence map, where the area with high perceptually critical level is the area that contains an object with a high confidence score. Given the feature map at the $k$th communication round, $F_i^{(k)}$ , the corresponding spatial confidence map is

\[C_i^{(k)} = \Phi_{generator}(F_i^{(k)}) \in [0, 1]^{H \times W}\tag1\label1\]

Since we consider multi-round collaboration, Where2comm iteratively updates the feature map by aggregating information from other agents. Once $F_i^{(k)}$is obtained, \eqref{1} is triggered to reflect the perceptually critical level at each spatial location. The proposed spatial confidence map answers a crucial question that was ignored by previous works.

Spatial confidence-aware communication

With the guidance of spatial confidence maps, the proposed communication module packs compact messages with spatially sparse feature maps and transmits messages through a sparsely-connected communication graph. To reduce the communication bandwidth without affecting perception, we leverage the spatial confidence map to select the most informative spatial areas in the feature map (where to communicate) and decide the most beneficial collaboration partners (who to communicate).

Message packing.

Message packing determines what information should be included in the to-besent message. The proposed message includes: i) a request map that indicates at which spatial areas the agent needs to know more; and ii) a spatially sparse, yet perceptually critical feature map.

Specifically, a binary selection matrix is used to represent each location is selected or not, where 1 denotes selected, and 0 elsewhere. For the message sent from the $i$th agent to the $j$th agent at the $k$th communication round, the binary selection matrix is

\[M_{i \rightarrow j}^{(k)} = \begin{cases} \Phi_{select}(C_i^{(k)}) \in \lbrace 0, 1 \rbrace ^{H \times W}, & k =0;\\ \Phi_{select}(C_i^{(k)} \odot (1 - C_j^{(k-1)})) \in \lbrace 0, 1 \rbrace ^{H \times W}, & k>0; \end{cases}\]

$\Phi_{select}(\cdot)$ is the selection function which targets to select the most critical areas conditioned on the input matrix, which represents the critical level at the certain spatial location. Then, the selected feature map is obtained as $Z_{i \rightarrow j}^{(k)} = M_{i \rightarrow j}^{(k)} \odot F_i^{(k)} \in R^{H \times W \times C}$

Communication graph construction.

Communication graph construction targets to identify when and who to communicate to avoid unnecessary communication that wastes the bandwidth. For the initial communication round, every agent in the system is not aware of other agents yet. To activate the collaboration, we construct a fully-connected communication graph. Every agent will broadcast its message to the rest of the system. For the subsequent communication rounds, we examine if the communication between agent i and agent j is necessary based on the maximum value of the binary selection matrix $M_{i \rightarrow j}^{(k)}$, i.e. if there is at least one patch is activated, then we regard the connection is necessary

Spatial confidence-aware message fusion

To fuse the features from the $j$th agent at the $k$th communication round, the cross-agent/ego attention weight for the $i$th agent is

\[W_{j \rightarrow i}^{(k)} = MHA_W(F_i^{(k)},Z_{j \rightarrow i}^{(k)}, Z_{i \rightarrow j}^{(k)}) \odot C_j^{(k)} \in R^{H \times W}\]

where $MHA_W(\cdot)$ is a multi-head attention applied at each individual spatial location, which outputs the scaled dot-product attention weight.Then, the feature map of the $i$th agent after fusing the messages in the kth communication round is

\[F_i^{(k+1)} = FFN\left( \sum_{j \in N(i) \cup \lbrace i \rbrace} \right W^{(k)}_{j \rightarrow i} \odot Z^{(k)}_{j \rightarrow i}) \in R^{H \times W \times D}\]

Compared to existing fusion modules that do not use attention mechanism [1] or only use agent-level attentions, the per-location attention mechanism adopted by the proposed fusion emphasizes the location-specific feature interactions.

Detection decoder

The detection decoder decodes features into objects, including class and regression output. Given the feature map at the $k$th communication round $F_i^{(k)} $ , the detection decoder $\Phi_{dec}(\cdot)$ generate the detections of $i$th agent by $\hat O_i^{(k)} = \Phi_{dec}(F_i^{(k)}) \in R^{H \times W \times 7}$ , where each location of $\hat O_i^{(k)}$ represents a rotated box with class $(c, x, y, h, w, cos \alpha, sin \alpha)$, denoting class confidence, position, size and angle.

Hong Huang