Model-Agnostic Multi-Agent Perception Framework

2023-01-26

Basic Information

Authors: Runsheng Xu, Weizhe Chen, Hao Xiang, Xin Xia, Lantao Liu, Jiaqi Ma

Organization: University of California, Los Angeles, CA, USA; Indiana University, Bloomington, IN, USA

Source: IEEE International Conference on Robotics and Automation (ICRA) 2023

Source Code: None

Content

Motivation

Existing fusion frameworks assume that all the collaborating agents share an identical model with the same parameters. This assumption is hard to satisfy in practice, particularly in autonomous driving.

Due to the distinct models used by the agents, the confidence scores provided by different agents can be systematically misaligned. Some agents may be over-confident, whereas others tend to be under-confident. Directly fusing bounding box proposals from neighboring agents using can result in poor detection accuracy due to the presence of overconfident and low-quality candidates.

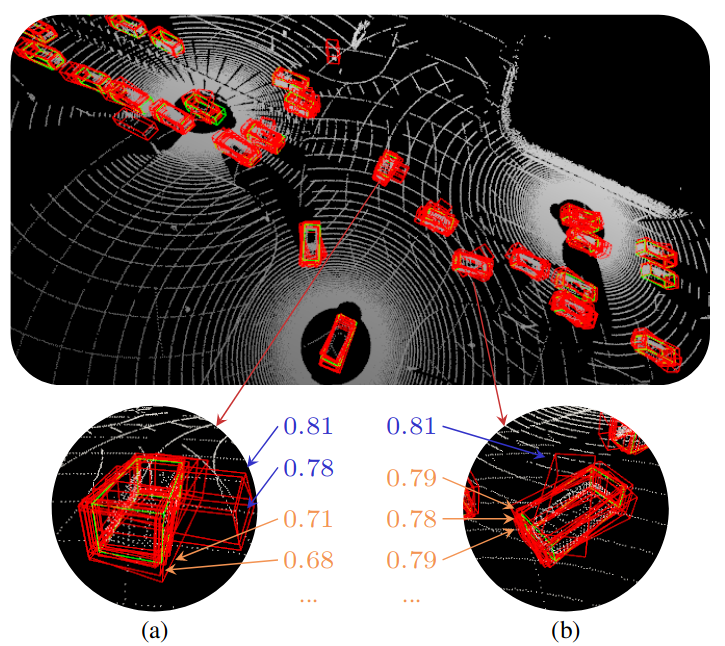
Figure 1. Ground truth (green) and bounding box candidates (red) produced by three connected autonomous vehicles. (a) Some agents have confidence scores that are systematically larger than others, e.g., the blue scores versus the orange scores. However, they might be confidently wrong, which mislead the fusion process. (b) Candidates with slightly lower confidence scores (orange) but higher spatial agreement with neighboring boxes can be better than a singleton with a higher confidence score (blue).

We propose a simple yet flexible confidence calibrator, called Doubly Bounded Scaling (DBS), to mitigate the misalignment. We also propose a corresponding bounding box aggregation algorithm, named Promote-Suppress Aggregation (PSA), that considers the confidence scores and the spatial agreement of neighboring boxes. Fig. 1 illustrates the importance of these two components.

Evaluation

Metric: We evaluate the detection accuracy in the range of $x \in [−140, 140]$m and $y \in [−40, 40]$m, centered at the ego-vehicle coordinate frame. The detection performance is measured with Average Precision (AP) at IoU = 0.7.

Evaluation setting: We evaluate our method under three different settings: 1) Homo Setting, where the detectors of agents are homogeneous with the same architecture and trained parameters. This setting has no confidence distribution gap and is used to demonstrate the performance drop when taking heterogeneity into account; 2) Hetero Setting 1, where the agents have the same model architecture but different parameters; 3) Hetero Setting 2, where the detector architectures are disparate.

Datasets

OPV2V

Result

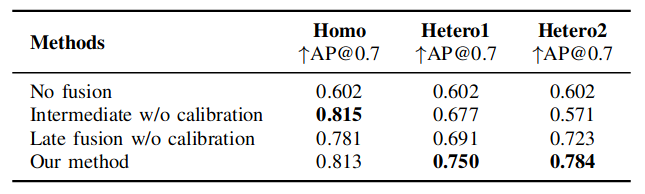
Table 1. object detection performance. Average Precision (AP) at IoU=0.7 on homo, hetero1, and hetero2 setting.

Method

Our goal is to develop a robust framework to handle the heterogeneity among agents while preserving confidentiality. The proposed model-agnostic collaborative perception framework is shown in Fig. 2, which can be divided into two stages. In the offline stage, we train a modelspecific calibrator. During the online phase, real-time on-road sensing information is calibrated and aggregated.

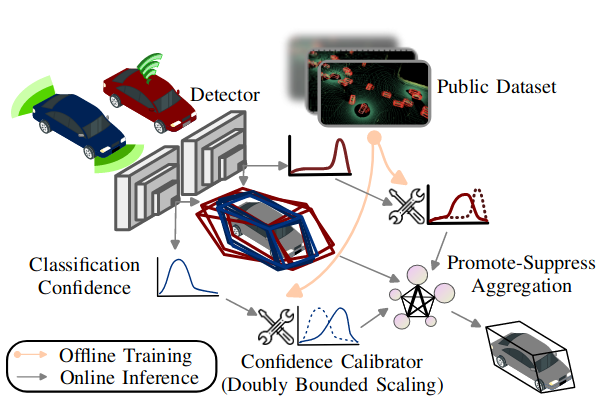
Figure 2. Overview of the proposed framework. Each agent trains its confidence calibrator (i.e., Doubly Bounded Scaling) on the same public dataset offline (orange arrows). Promote-Suppress Aggregation yields the final detection result, considering the spatial information and calibrated confidence of bounding boxes given by connected autonomous vehicles

Classification Confidence Calibration

To eliminate the bias brought by the system heterogeneity, the models need to be well-calibrated. If the confidence scores can imply the likelihood of correct prediction, for example, $80%$ confidence leads to $80%$ accurate predictions, this model is well-calibrated.

Scaling-Based Confidence Calibration.

The goal of scaling-based confidence calibration is to learn a parametric scaling function (i.e., calibrator) $c_{\theta} (\hat s) [0,1] \rightarrow [0,1]$ on a calibration dataset to transform the uncalibrated confidence scores into well-calibrated ones $s$. we optimize the parameters $\theta$ of the calibrator by gradient descent on the binary cross entropy loss

\[l_{CE} = -y_nlog(s_n) - (1 - y_n)log(1 - s_n),\]

where $s_n = c_\theta (\hat s)$. Designing a suitable calibrator for our application requires satisfying three conditions: (a) The scaling function needs to be monotonically non-decreasing as a higher confidence score is supposed to indicate a higher expected accuracy; (b) The scaling function should be relatively smooth to avoid over-fitting to the calibration set; (c) The scaling function is supposed to be doubly bounded, meaning that it maps a confidence interval [0, 1] to the same [0, 1] range.

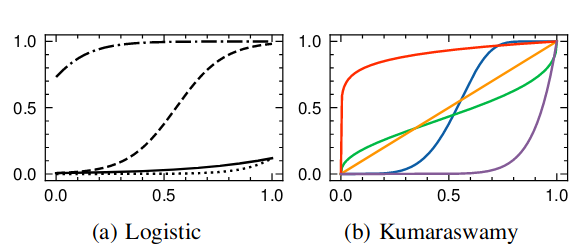
Figure 3. Scaling functions with various parameters that follow (a) the logistic form and (b) the Kumaraswamy CDF. Note that, in (b), the “inversesigmoid” shape (green curve, a = 0.4, b = 0.4) and the identity map (orange curve, a = 1, b = 1) are not in the logistic family.

The most popular scaling methods are arguably Platt Scaling and Temperature Scaling. Platt Scaling uses the logistic family as the calibrator:

\[c_{Platt}(\hat s; a, b) = \frac{1}{1 + exp(-(a\hat s + b))},\]

Fig. 3 shows several scaling functions from this family. Platt Scaling can fail if its parametric assumptions are not met. For example, we cannot learn an “inverse-sigmoid” (see the green curve in Fig. 3b) scaling function within this family.

We propose to use the Kumaraswamy Cumulative Density Function (CDF) that meets all the three constraints while being sufficiently flexible. Specifically, we learn a scaling function with the following form:

\[c(\hat s; a, b) = 1 - (1 - \hat s ^ a)^b,\]

where $a > 0$ and $b > 0$ are the parameters.

Promote-Suppress Aggregation (PSA)

To select the high-score bounding boxes with many confident neighbors, we propose Promote-Suppress Aggregation (PSA), which takes into account both the regression and classification confidences. Fig. 4 illustrates the idea of PSA. We first construct a spatial graph of bounding box candidates based on Intersectionover-Union (IoU) values and the confidence scores.

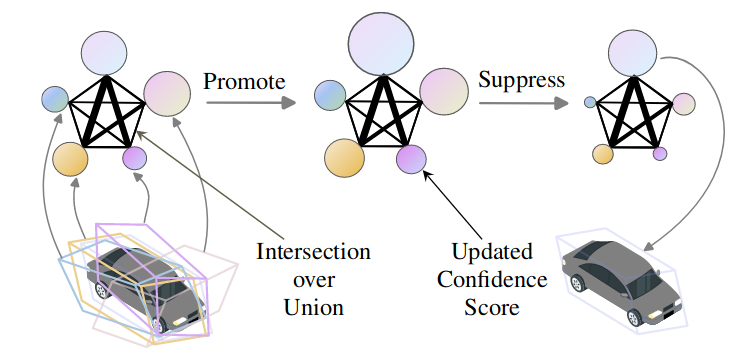
Figure 4. Illustration of Promote-Suppress Aggregation. The size of a node indicates the confidence score of the bounding box and the edge width represents the Intersection-over-Union of two boxes.

Algorithm 1 shows how PSA computes the index set. We can select multiple candidates if $\epsilon \in (0, 1]$ is large and $\phi$ is small. In our application, however, one component typically contains only one object/vehicle, so we use a small $\epsilon$ and $\phi$ = 0.5.