Basic Information

Cite by @article{wang2020tackling, title={Tackling the Objective Inconsistency Problem in Heterogeneous Federated Optimization}, author={Wang, Jianyu and Liu, Qinghua and Liang, Hao and Joshi, Gauri and Poor, H Vincent}, journal={Advances in Neural Information Processing Systems}, volume={33}, year={2020} }

Authors Jianyu Wang, Qinghua Liu , Hao Liang, Gauri Joshi, H. Vincent Poor

Organization Carnegie Mellon University, Princeton University

Source Advances in Neural Information Processing Systems 2020

Source Code https://github.com/JYWa/FedNova

Content

Motivation

There is heterogeneity in the Number of Local Updates in Federated Learning, which causes objective inconsistency. However, none of prior works provides insight into the convergence of algorithms when the number of local update heterogeneity happens.

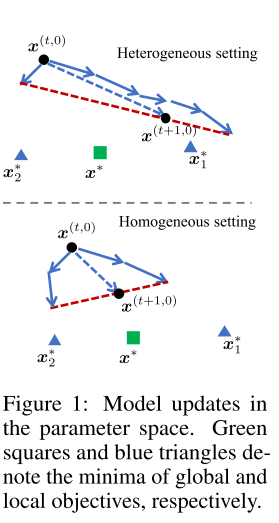
As we know, in federated learning, a total of \(m\) clients aim to jointly solve the following optimization problem: \(\min_x [F(x) = \sum_{i=1}^m p_i F_i(x)] \tag{1}\label1\) where \(p_i = \frac{n_i}{n}\), and \(F_i(x) = \frac{1}{n_i}\sum_{xi\in D_i}f_i(x;\xi)\) is the local objective function at thr \(i\)-th client. And \(\xi\) is a data sample from local dataset \(D_i\).

In practice, there is heterogeneity in the number of local updates due to distribution skew. Author sets \(\tau_i\) as the number of local SGD iteration in \(i\)-th client, such that \(\tau_i = [\frac{En_i}{B}]\). Therefore, take FedAvg for an example, the shared global model is updated as following: \(x^{(t+1, 0)} - x^{(t, 0)} = \sum_{i=1}^{m}p_i\Delta_i^{(t)} = -\sum_{i=1}^{m}p_i\eta\sum_{k=0}^{\tau_i-1}g_i(x_i^{(t,k)}) \tag{2}\label2\)

Where \(x_i^{(t,k)}\) denotes client \(i\)’s model after the \(k\)-th local update in the \(t\)-th communication round and \(\Delta_i^{(t)} = x_i^{(t,\tau_i)} - x_i^{(t,0)}\). \(\eta\) is the client learning rate and \(g_i(\cdot)\) represents the stochastic gradient over a mini-batch of \(B\) samples.

Suppose that the local objective functions are \(F_i(x) = \sum_{i=1}^m\frac1{2m}||x-e_i||^2, which\quad is \quad minimized \quad by \quad x^* = \frac1m \sum_{i=1}^me_i \tag3\label3\) where \(e_i\) is an arbitrary vector. It can be shown that FedAvg will converge to \(\widetilde{x}^* = \lim_{T\rightarrow\infty} x^(T,0) = \sum_{i=1}^m\frac{\tau_i}{\tau}e_i\), which minimizes the surrogate objective: \(\widetilde{F}(x) = \sum_{i=1}^m\frac{\tau_i}{\tau}F_i(x)\). While FedAvg aims at optimizing \(F(x)\), it actually converges to the optimum of a surrogate objective \(\widetilde{F}(x)\).

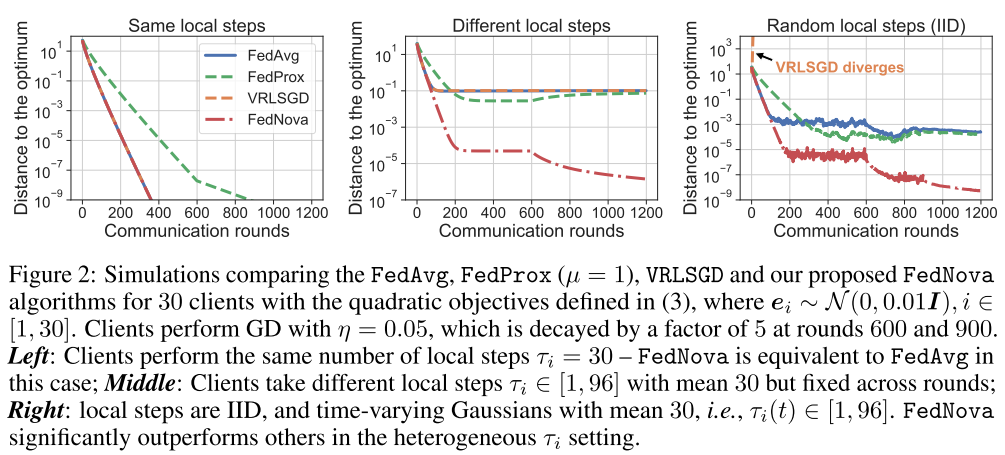
As figure shown, FedProx and VRLSGD also cause bias due to objective Inconsistency.

Evaluation

Metric: Training loss, Test Accuracy

Datasets

Logistic Regression on a Synthetic Federated Dataset and DNN trained on a Non-IID partitioned CIFAR-10 dataset.

Result

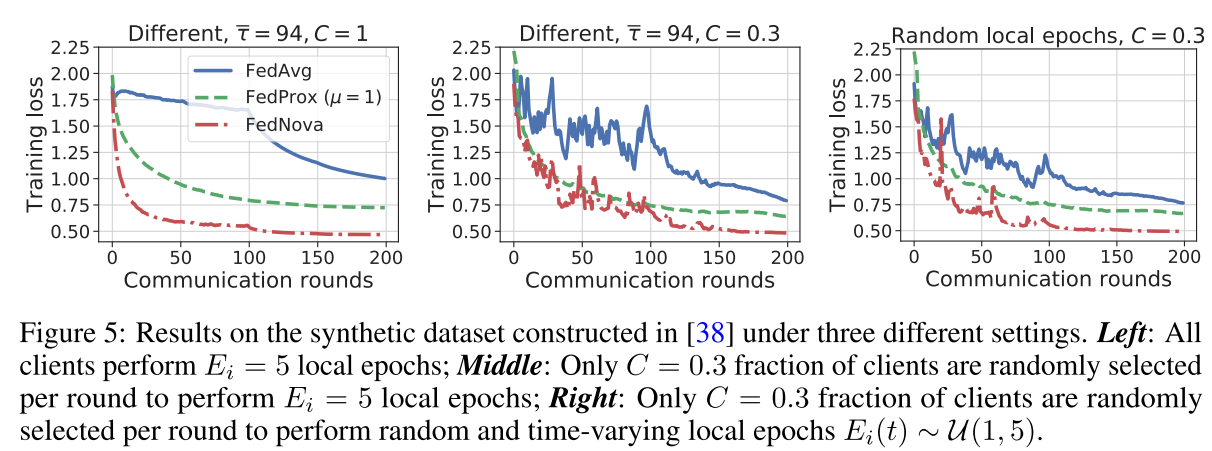
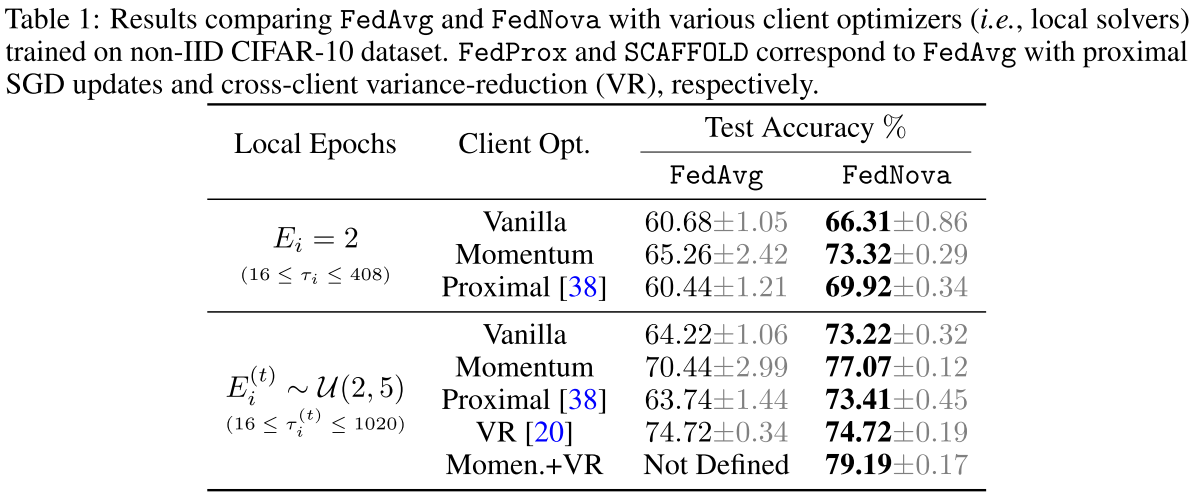
Method

The authors proposed an analysis framework to understand bias due to objective Inconsistency and proposed Federated Normalized Averaging Algorithm(FedNova) to solve this problem.

Analysis Framework

Rewrite \eqref{2} to following update form. \(x^{(t+1, 0)} - x^{(t, 0)} = -\tau_{eff} \sum_{i=1}^{m} w_i \cdot \eta d_i^{(t)}, \quad which \quad optimizes \quad \widetilde{F}(x) = \sum_{i=1}^{m}w_iF_i(x) \tag4\label4\)

the three key elements \(\tau_{eff}, w_i, d_i^{(t)}\) of this update rule take different forms for different algorithms.

1) Normalized gradient \(d_i^{(t)}\): \(d_i^{(t)} = \frac{ G_i^{(t)}a_i}{||a_i||}\), where \(G_i^{(t)} = [g_i(x_i^{(t,0)}), g_i(x_i^{(t,1)}), \dots, g_i(x_i^{(t,\tau_i)})]\) stacks all stochastic gradients in the \(t\)-th round. \(a_i\in \mathbf{R}^{\tau_i}\) (weight of each gradient). In FedAvg, \(a_i = [1,1,\dots, 1], ||a_i|| = \tau_i\) 2) Aggregation weights \(w_i\) 3) Effective number os step \(\tau_{eff}\): The average number of local SGD step per communication round is \(\hat{\tau} = \sum_i^m\frac{\tau_i}{m}\). However, the server can control the effect the aggregated updates by setting the parameter \(\hat{\tau}\).

For previous algorithms: \(x^{(t+1, 0)} - x^{(t, 0)} = \sum_{i=1}^{m}p_i\Delta_i^{(t)} = -\sum_{i=1}^{m}p_i||a_i||\cdot\frac{G_i^{(t)}a_i}{||a_i||} \\ = - \underbrace{(\sum_{i=1}^{m}p_i||a_i||)}_{\tau_{eff}} \sum_{i=1}^{m}\eta \underbrace{(\frac{p_i||a_i||}{\sum_{i=1}^{m}p_i||a_i||})}_{w_i} \underbrace{(\frac{ G_i^{(t)}a_i}{||a_i||})}_{d_i} \tag5\label5\)

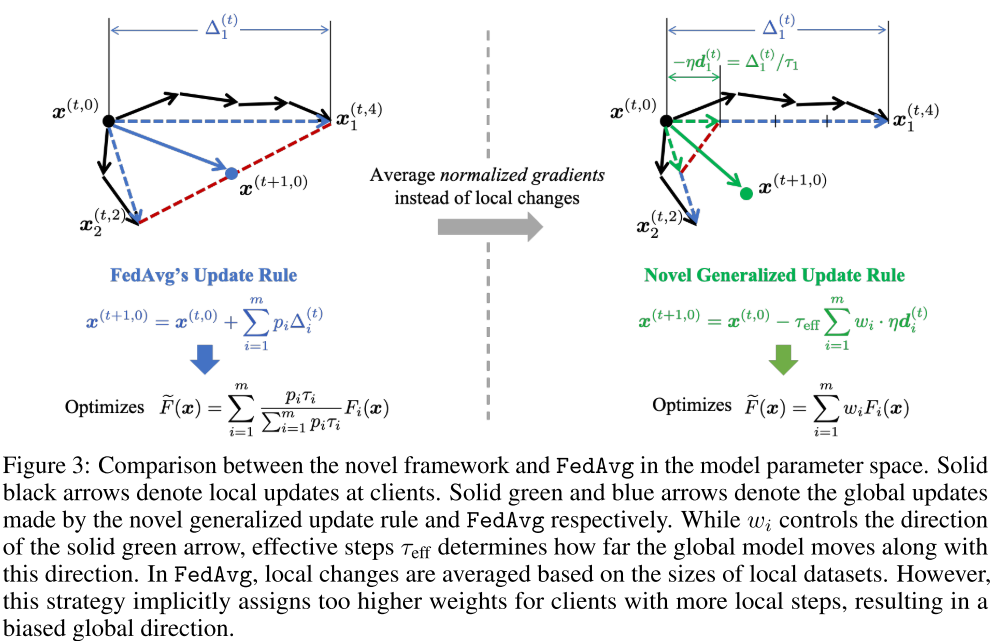
For FedAvg, above figure shows the difference. The left figure shows the original aggregation function in FedAvg.

Convergence Analysis

Assumption 1:(L-Smoothness) \(||\nabla F_i(x) - \nabla F_i(y)|| \le L||x-y||\)

Assumption 2:(Unbiased Gradient and Bounded Variance) \(\mathbb{E}_\xi[||g_i(x|\xi)\nabla F_i(x)||^2] \le \sigma^2 L||x-y||\)

Assumption 3:(Bounded Dissimilarity) \(\exists \beta^2\ge 0, \kappa^2\ge 0 s.t. \sum_{i=1}^{m}w_i||\nabla F_i(x)||^2 \le \beta^2||\sum_{i=1}^{m}w_i\nabla F_i(x)||^2 + \kappa^2\)

Base above assumptions, author gets following theorem:

Theorem 1(Convergence to \(\widetilde{F}(x)\) Stationary Point). Under assumptions 1 to 3, any fedrated optimizaition algorithm that follows the update rule \eqref{4}, will converge to a stationary point. if learning rate \(\eta = \sqrt{\frac{m}{\hat{\tau}T}}\), then the optimization error will be bounded as follows: \(\min_{t\in[T]} \mathbb{E}|| \nabla \widetilde{F}(x^{(t,0)})||^2 \le O(\frac{\hat{\tau}\eta}{m\tau_{eff}}) + O(\frac{A\eta\sigma^2}{m}) + O(B\eta^2\sigma^2) + O(C\eta^2\kappa^2) \tag6\)

Where A, B, C are defined as follows: \(A = m\tau_{eff}\sum_{i=1}^m \frac{w_i^2||a_i||_2^2}{||a_i||_1^2}, B = \sum_{i=1}^m w_i(||a_i||_2^2 - a_{i,-1}^2), C = \max_i \{||a_i||_1^2 - ||a_i||_1a_{i,-1}\} \tag7\) \(a_{i,-1}\) is the last element in the vector \(a_i\).

FedNova: Federated Normalized Averaging Algorithm

where \(\tau^{(t)}_{eff} = \sum_{i=1}^{m} p_i\tau_i^{(t)}, d_i^{(t)} = \frac{ G_i^{(t)}a_i}{||a_i||}\).

Comments

Pros

1. Solve the heterogeneity in the Number of Local Updates in Federated Learning
2. Proposed a general framework which can guarantee the convergence to the stationary point.

Cons

(need further experiment)

Further work

Extending the theoretical framework to adaptive optimization methods or gossip-based training method.

Comments

(need further experiment)